【题目】如图,正方形ABCD的顶点A,B在函数y= ![]() (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
①当k=2时,正方形A′B′C′D′的边长等于 .
②当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是 . 
参考答案:
【答案】![]() ;
;![]() ≤x≤18
≤x≤18
【解析】解:(1)如图,过点A′作AE⊥y轴于点E,过点B′⊥x轴于点F,则∠A′ED′=90°. 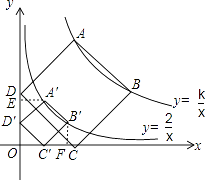
∵四边形A′B′C′D′为正方形,
∴A′D′=D′C′,∠A′D′C′=90°,
∴∠OD′C′+∠ED′A′=90°.
∵∠OD′C′+∠OC′D′=90°,
∴∠ED′A′=∠OC′D′.
在△A′ED′和△D′OC′中,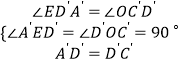 ,
,
∴△A′ED′≌△D′OC′(AAS).
∴OD′=EA′,OC′=ED′.
同理△B′FC′≌△C′OD′.
设OD′=a,OC′=b,则EA′=FC′=OD′=a,ED′=FB′=OC′=b,
即点A′(a,a+b),点B′(a+b,b).
∵点A′、B′在反比例函数y= ![]() 的图象上,
的图象上,
∴ ![]() ,解得:
,解得: ![]() 或
或 ![]() (舍去).
(舍去).
在Rt△C′OD′中,∠C′OD′=90°,OD′=OC′=1,
∴C′D′= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
2)设直线A′B′解析式为y=k1x+b1 , 直线C′D′解析式为y=k2+b2 ,
∵点A′(1,2),点B′(2,1),点C′(1,0),点D′(0,1),
∴有 ![]() 和
和 ![]() ,
,
解得: ![]() 和
和 ![]() .
.
∴直线A′B′解析式为y=﹣x+3,直线C′D′解析式为y=﹣x+1.
设点A的坐标为(m,2m),点D坐标为(0,n).
当A点在直线C′D′上时,有2m=﹣m+1,解得:m= ![]() ,
,
此时点A的坐标为( ![]() ,
, ![]() ),
),
∴k= ![]() ×
× ![]() =
= ![]() ;
;
当点D在直线A′B′上时,有n=3,
此时点A的坐标为(3,6),
∴k=3×6=18.
综上可知:当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围为 ![]() ≤x≤18.
≤x≤18.
所以答案是: ![]() ≤x≤18.
≤x≤18.
【考点精析】关于本题考查的反比例函数的性质和正方形的性质,需要了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙O的弦,点C是
 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD;
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°; 
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ,求
,求  的值.
的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x﹣3经过B、C两点.

(1)求抛物线的解析式;
(2)过点C作直线CD⊥y轴交抛物线于另一点D,点P是直线CD下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点P作PE⊥x轴于点E,PE交CD于点F,交BC于点M,连接AC,过点M作MN⊥AC于点N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,连接PC,过点B作BQ⊥PC于点Q(点Q在线段PC上),BQ交CD于点T,连接OQ交CD于点S,当ST=TD时,求线段MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )

A.
B.
C.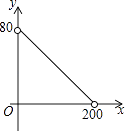
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.

(1)求这个月晴天的天数.
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其它费用,结果取整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
相关试题

