【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
参考答案:
【答案】
(1)
证明:ED=EC=CF,
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,∠BCA=60°,BE=AF,EC=CF,
∴△CEF是等边三角形,
∴EF=EC,∠CEF=60°,
又∵ED=EC,
∴ED=EF,
∵△ABC是等腰三角形,∠BCA=60°,
∴△ABC是等边三角形,
∴∠CAF=∠CBA=60°,
∴∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE,
∵∠CAF=∠CEF=60°,
∴A、E、C、F四点共圆,
∴∠AEF=∠ACF,
又∵ED=EC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
在△EDB和△FEA中,
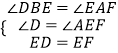 (AAS)
(AAS)
∴△EDB≌△FEA,
∴DB=AE,BE=AF,
∵AB=AE+BE,
∴AB=DB+AF
(2)
证明:AB=BD﹣AF;
延长EF、CA交于点G,
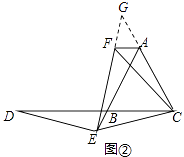
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,
∴△CEF是等边三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,∠EFC=∠BAC=60°,
∵∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∵∠FCG=∠ECD,∠D=∠ECD,
∴∠D=∠FEA,
由旋转的性质,可得
∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°,
在△EDB和△FEA中,
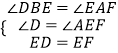 (AAS)
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∴BD=FA+AB,
即AB=BD﹣AF
(3)
证明:如图③,
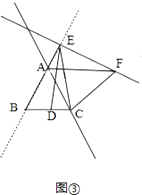 ,
,
ED=EC=CF,
∵△BCE绕点C顺时针旋转60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,BC=AC,
∴△CEF是等边三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,
∵AB=AC,BC=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,
又∵∠CBE=∠CAF,
∴∠CAF=60°,
∴∠EAF=180°﹣∠CAF﹣∠BAC
=180°﹣60°﹣60°
=60°
∴∠DBE=∠EAF;
∵ED=EC,
∴∠ECD=∠EDC,
∴∠BDE=∠ECD+∠DEC=∠EDC+∠DEC,
又∵∠EDC=∠EBC+∠BED,
∴∠BDE=∠EBC+∠BED+∠DEC=60°+∠BEC,
∵∠AEF=∠CEF+∠BEC=60°+∠BEC,
∴∠BDE=∠AEF,
在△EDB和△FEA中,
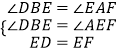 (AAS)
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∵BE=AB+AE,
∴AF=AB+BD,
即AB,DB,AF之间的数量关系是:
AF=AB+BD
【解析】(1)首先判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE;然后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,AB=AE+BF,所以AB=DB+AF.(2)首先判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,∠FCG=∠FEA,再根据∠FCG=∠EAD,∠D=∠EAD,可得∠D=∠FEA;然后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,EB=AF,进而判断出AB=BD﹣AF即可.(3)首先根据点E在线段BA的延长线上,在图③的基础上将图形补充完整,然后判断出△CEF是等边三角形,即可判断出EF=EC,再根据ED=EC,可得ED=EF,∠CAF=∠BAC=60°,再判断出∠DBE=∠EAF,∠BDE=∠AEF;最后根据全等三角形判定的方法,判断出△EDB≌△FEA,即可判断出BD=AE,EB=AF,进而判断出AF=AB+BD即可.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)如图1,AB<AD,
①求证:四边形BEDF是菱形;
②若AB=4,AD=8,求四边形BEDF的面积;
(2)如图2,若AB=8,AD=4,请按要求画出图形,并直接写出四边形BEDF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD.有下列四个结论:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直线MB垂直平分线段CD;(4)四边形ABCD是轴对称图形.其中正确结论的个数为( )
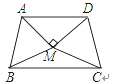
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=
 x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y= x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )

A.
 B.
B.  C.
C.  D. 不能确定
D. 不能确定
相关试题

