Question

【题目】如图，⊙的圆心在反比例函数的图像上，且与轴、轴相切于点、，一次函数的图像经过点，且与轴交于点，与⊙的另一个交点为点.

（1）求的值及点的坐标；

（2）求长及的大小；

（3）若将⊙沿轴上下平移，使其与轴及直线均相切，求平移的方向及平移的距离.

Answer 1

【答案】（1） ，（-3,0；（2）3,60°；（3）向上平移3个单位或向下平移1个单位；

【解析】试题分析：（1）如图1中，连接AC、AB．首先证明四边形ABOC是正方形，求出点C坐标，利用待定系数法即可解决问题．
（2）如图2中，连接BC、BE，作AM⊥CE于M．在Rt△DOC中，由tan∠CDO=，推出∠CDO=30°，由AC∥BD，推出∠ECA=∠CDO=30°，∠CAM=60°，
由AM⊥CE，推出∠CAM=∠EAM=60°，推出∠CAE=120°，在Rt△AMC中，根据CM=ACcos30°=，推出CE=2CM=3，可得∠CBE=∠CAE=60°，由此即可解决问题．
（3）分两种情形求解如图3中，当⊙A″与直线y=相切于点E，AB与直线CD交于点K，想办法求出AA″，即可解决问题．同法求出AA′．

试题解析：（1）如图1中，连接AC、AB．

∵⊙A与x轴、y轴相切于点B、C，
∴AC⊥OC，AB⊥OB，AC=AB，四边形ABOC是正方形，设A（m，m），
∵点A在y=上，
∴m2=3，
∵m＞0，
∴点A坐标（， ），
∴OC=，
∴点C坐标（0， ），
∵一次函数y=x+b的图象经过点C，
∴b=，
∴一次函数的解析式为y=，

令y=0得x=-3，
∴D（-3，0），b=．
（2）如图2中，连接BC、BE，作AM⊥CE于M．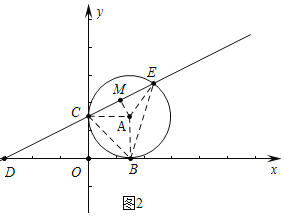

在Rt△DOC中，∵tan∠CDO=，
∴∠CDO=30°，
∵AC∥BD，
∴∠ECA=∠CDO=30°，∠CAM=60°，
∵AM⊥CE，
∴∠CAM=∠EAM=60°，
∴∠CAE=120°，
在Rt△AMC中，CM=ACcos30°=，
∴CE=2CM=3，
∴∠CBE=∠CAE=60°．
（3）如图3中，

①当⊙A″与直线y=相切于点E，AB与直线CD交于点K，
∵AB∥OC，
∴∠A″KE=∠DKB=∠DCO=60°，
在Rt△A″EK中，A″E=，A″K=A″E÷cos30°=2，
在Rt△CKA中，AK=CAtan30°=1，
∴AA″=A″K+AK=1+2=3，
∴⊙A向上平移3的单位⊙A与y轴及直线y=均相切．
②同理可得⊙A向下平移1个单位⊙A与y轴及直线y=均相切．