Question

【题目】在△ABC中，P为边AB上一点．

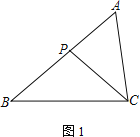
(1) 如图1，若∠ACP＝∠B，求证：AC2＝AP·AB；

(2) 若M为CP的中点，AC＝2，

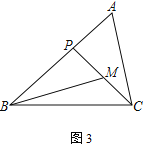
① 如图2，若∠PBM＝∠ACP，AB＝3，求BP的长；

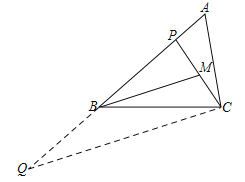
② 如图3，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．

Answer 1

【答案】（1）证明见解析；（2）①；②

【解析】试题分析：（1）根据已知条件易证△ACP∽△ABC，由相似三角形的性质即可证得结论；（2）①如图，作CQ∥BM交AB延长线于Q，设BP＝x，则PQ＝2x，易证△APC∽△ACQ，所以AC2＝AP·AQ，由此列方程，解方程即可求得BP的长；②如图：作CQ⊥AB于点Q，作CP0＝CP交AB于点P0，再证△AP0C∽△MPB，（2）的方法求得AP0的长，即可得BP的长．

试题解析：（1）证明：∵∠ACP＝∠B，∠BAC＝∠CAP，

∴△ACP∽△ABC，

∴AC：AB＝AP：AC，

∴AC2＝AP·AB；

（2）①如图，作CQ∥BM交AB延长线于Q，设BP＝x，则PQ＝2x

∵∠PBM＝∠ACP，∠PAC＝∠CAQ，

∴△APC∽△ACQ，

由AC2＝AP·AQ得：22＝（3－x）（3＋x），∴x＝

即BP＝；

②如图：作CQ⊥AB于点Q，作CP0＝CP交AB于点P0，

∵AC＝2，∴AQ＝1，CQ＝BQ＝，

设AP0=x，P0Q＝PQ＝1－x，BP＝－1＋x，

∵∠BPM＝∠CP0A，∠BMP＝∠CAP0，

∴△AP0C∽△MPB，∴，

∴MPP0C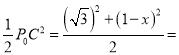＝AP0BP＝x（－1＋x），

解得x＝

∴BP＝－1＋＝．