【题目】综合题。
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.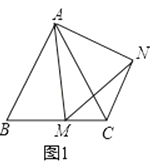
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.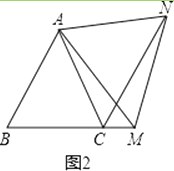
参考答案:
【答案】
(1)
证明:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中, 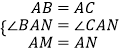
∴△ABM≌△ACN(SAS),
∴∠ACN=∠ABM=60°,
∵∠ACB=60°
∴∠BCN+∠ABM=180°;
∴CN∥AB
(2)
证明:成立,
理由如下:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠CAM=∠CAM+∠MAN,
∴∠BAM=∠CAN
在△ABM和△ACN中, 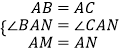 ,
,
∴△ABM≌△ACN(SAS),
∴∠ACN=∠ABM=60°,
∵∠ACB=60°
∴∠BCN+∠ABM=180°;
∴CN∥AB
【解析】(1)利用等边三角形的性质得出AB=AC,AM=AN,∠BAC=∠MAN,进而得出∠BAM=∠CAN,即可判断出△ABM≌△ACN(SAS),得出∠ACN=∠ABM=60°,进而得出∠BCN+∠ABM=180°即可得出结论;(2)同(1)的方法即可得出结论.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD.
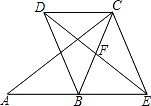
(1)求证:四边形DBEC是平行四边形.
(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中: ①当BE=时,四边形BECD是矩形,试说明理由;
②当BE=时,四边形BECD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)2n+1+2(﹣2)2n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为度.
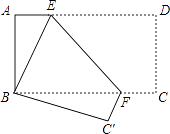
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子从左到右的变形是因式分解的是( )
A. a2+4a-21=a(a+4)-21
B. (a-3)(a+7)=a2+4a-21
C. a2+4a-21=(a-3)(a+7)
D. a2+4a-21=(a+2)2-25
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A.44×108
B.4.4×109
C.4.4×108
D.4.4×1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣x3ya与xby是同类项,则a+b的值为( )
A.2
B.3
C.4
D.5
相关试题

