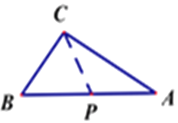
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.



参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ;②
;②![]() ③
③![]() ④
④![]()
【解析】试题分析:(1)根据已知可得AC的长,AP的长,从而可得PC的长,在直角三角形BCP中利用勾股定理即可求得;
(2)作PH⊥AB,由已知可得PH=PC=4t-8,PB=14-4t,在Rt△BPH中,由勾股定理即可得;
(3)分情况计谋即可得.
试题解析:(1)点P在AC上,∵∠ACB=90°,BC=6,AB=10,∴AC=8,
AP=4t,CP=8-4t,
又∵PA=PB,∴![]() ,
,
t=![]() ;
;
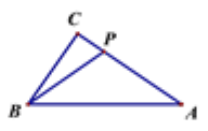
(2)点P在∠BAC的角平分线上,作PH⊥AB,
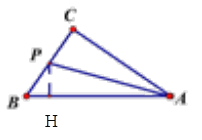
∴PC=PH=4t-8,PB=14-4t,
可证△ACP≌△AHP, ∴AH=BC=8,∴BH=2,
在Rt△BPH中, ![]() ,即
,即![]() ,
,
t=![]() ;
;
(3)①当PC=BC=6时,此时AP=AC-PC=2,∴t=![]() =
=![]() ;
;

②当PC=BC时,作CH⊥AB,则有PH=BH,由AC﹒BC=AB﹒CH,可得CH=4.8,由勾股定理则有BH=3.6,所以PB=7.2,由已知则有BP=4t-14,由点P运动的时间以及速度,可得BP=4t-14,
所以4t-14=7.2,解得 ![]() ;
;
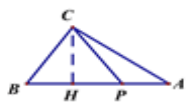
③当PC=BP时,作CH⊥AB,由AC﹒BC=AB﹒CH,可得CH=4.8,由勾股定理则有BH=3.6,
由点P运动的时间以及速度,可得BP=4t-14, 所以PH=4t-14-3.6=4t-17.6,
由勾股定理可得CH2+PH2=PC2 ,即4.82+(4t-17.6)2=(4t-14)2 ,解得![]() ;
;
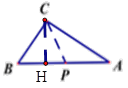
④当BC=BP时,此时BP=4t-14,所以4t-14=6,解得![]() ,
,
综上可知,当t为![]() 、
、![]() 、
、![]() 或
或![]() 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.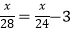
B.
C.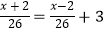
D.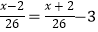
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根,求这个直角三角形的斜边长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点在格点上.

(1)画出△A1B1C1,使它与△ABC关于直线a对称;
(2)求出△A1B1C1的面积.
(3)在直线a上画出点P,使PA+PC最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-mx-2=0.
(1)若-1是方程的一个根,求m的值和方程的另一个根.
(2)对于任意实数m , 判断方程根的情况,并说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】把点P从数轴的原点开始,向右移动2个单位长度,再向左移动7个单位长度,此时点P所表示的数是 .
相关试题

