【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
参考答案:
【答案】(1)证明见解析;(2)60°.
【解析】
试题分析:(1)由∠ABC=90°就可以求出∠CBF=90°,由SAS就可以得出△ABE≌△CBF;
(2)由∠CAE=30°就可以求出∠BAE=15°,就可以得出∠BCF=15°,由条件可以求出∠ACB=45°,进而可以求出∠ACF的度数.
试题解析:(1)证明:∵∠ABC=90°,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
 ,
,
∴△ABE≌△CBF(SAS);
(2)∵△ABE≌△CBF,
∴∠BAE=∠BCF.
∵∠ABC=90°,AB=CB,
∴∠BCA=∠BAC=45°.
∵∠CAE=30°,
∴∠BAE=15°,
∴∠BCF=15°.
∵∠ACF=∠BCF+∠ACB,
∴∠ACF=15°+45°=60°.
答:∠ACF的度数为60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
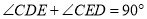 ,EM平分
,EM平分 ,并与CD边交于点M.DN平分
,并与CD边交于点M.DN平分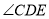 ,
,并与EM交于点N.
(1)依题意补全图形,并猜想
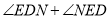 的度数等于 ;
的度数等于 ;(2)证明以上结论.
证明:∵ DN平分
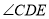 ,EM平分
,EM平分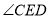 ,
, ∴
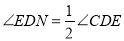 ,
,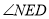 = .
= .(理由: )
∵
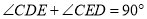 ,
,∴
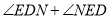 = ×(∠ +∠ )= ×90°= °.
= ×(∠ +∠ )= ×90°= °.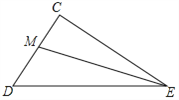
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.
B.
C.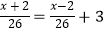
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.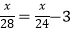
B.
C.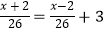
D.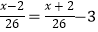
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根,求这个直角三角形的斜边长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点在格点上.

(1)画出△A1B1C1,使它与△ABC关于直线a对称;
(2)求出△A1B1C1的面积.
(3)在直线a上画出点P,使PA+PC最小.
相关试题

