【题目】(1)已知:甲篮球队投3分球命中的概率为![]() ,投2分球命中的概率为
,投2分球命中的概率为![]() ,某场篮球比赛在离比赛结束还有1min,时,甲队落后乙队5分,估计在最后的1min,内全部投3分球还有6次机会,如果全部投2分球还有3次机会,请问选择上述哪一种投篮方式,甲队获胜的可能性大?说明理由.
,某场篮球比赛在离比赛结束还有1min,时,甲队落后乙队5分,估计在最后的1min,内全部投3分球还有6次机会,如果全部投2分球还有3次机会,请问选择上述哪一种投篮方式,甲队获胜的可能性大?说明理由.
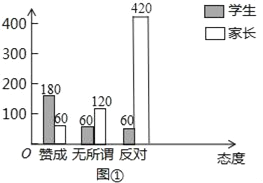
(2)现在“校园手机”越来越受到社会的关注,为此某校九年级(1)班随机抽查了本校若干名学生和家长对中学生带手机现象的看法,统计整理并制作了统计图(如图所示,图②表示家长的三种态度的扇形图)

1)求这次调查的家长人数,并补全图①;
2)求图②表示家长“赞成”的圆心角的度数;
3)从这次接受调查的家长来看,若该校的家长为2500名,则有多少名家长持反对态度?
参考答案:
【答案】(1) 应选择投3分球;(2)①补图见解析;②36°;③有1750名家长持反对态度.
【解析】试题分析:(1)根据已知条件可得3分求可能得![]() 分,投2分球可能得
分,投2分球可能得![]() ,再计算出结果即可,
,再计算出结果即可,
(2)先求出这次调查的家长人数,再减去赞成和无所谓的人数即可,先求出家长”赞成”的人数所占的百分比,再用360°乘以百分比即可,
(3)用该校的家长人数乘以持反对态度的家长所占的百分比即可.
试题解析:(1)∵甲篮球队投3分球命中的概率为![]() ,投2分球命中的概率为
,投2分球命中的概率为![]() ,在最后的1min内全部投3分球还有6次机会,如果全部投2分球还有3次机会,
,在最后的1min内全部投3分球还有6次机会,如果全部投2分球还有3次机会,
∴投3分球可能得![]() ×6×3=6(分)
×6×3=6(分)
投2分球可能得![]() ×3×2=4(分),
×3×2=4(分),
∴应选择投3分球,
(2)
1)这次调查的家长人数是:120÷20%=600人,
则反对的家长人数是:600﹣60﹣120=420人,
如图:
2)∵家长“赞成”的人数所占的百分比是, ![]() ×100%=10%,
×100%=10%,
∴表示家长“赞成”的圆心角的度数是360°×10%=36°,
3)若该校的家长为2500名,则持反对态度的家长有2500×(1﹣10%﹣20%)=1750人,
答:有1750名家长持反对态度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算 (﹣1)2×(﹣23)﹣(﹣4)÷2×

(2)先化简,再求值已知2(3a2b﹣5ab2)﹣3(2a2b﹣3ab2),其中a=﹣1,b=3.
(3)解方程:3(x﹣3)+1=x﹣(2x﹣1)
(4)解方程:
 ﹣
﹣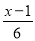 =2
=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径长为R=5,弦AB 与弦CD平行,他们之间距离为7,AB=6求:弦CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有以下几何图形:①线段;②角;③等腰三角形;④直角三角形;⑤梯形;⑥平行四边形,其中一定是轴对称图形的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=
 (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;② ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )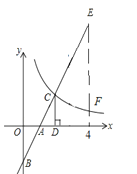
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有

A. ①②③ B. ①③④ C. ②③ D. ①②③④
相关试题

