【题目】二次函数![]() 的图象经过点(2,1),(0,1).
的图象经过点(2,1),(0,1).
(1)求该二次函数的表达式及函数图象的顶点坐标和对称轴;
(2)若点P![]() ),Q
),Q![]() )在抛物线上,试判断
)在抛物线上,试判断![]() 与
与![]() 的大小.(写出判断的理由)
的大小.(写出判断的理由)
参考答案:
【答案】(1) 顶点坐标为(1,-1),对称轴为 直线x=1;(2)见解析.
【解析】(1)利用待定系数法求出函数的解析式,然后根据配方法求出即可;
(2)先求得P、Q所处的位置,然后根据抛物线的性质即可判断.
(1)根据题意,得8+2b+c=1且c=1,解得b=-4,
所以该二次函数的表达式是![]() .
.
将![]() 配方得
配方得![]()
所以该二次函数图象的顶点坐标为(1,-1),
对称轴为过点(1,-1)平行于y轴的直线; (或:对称轴为直线x=1)
(2)∵![]() >
>![]() >1,
>1,
∴P、Q都在对称轴的右边,
又∵2>0,函数的图象开口向上,在对称轴的右边y随x的增大而增大,
∴![]() <
<![]() (如直接代入计算出y1与y2,并比较大小正确参照给分)
(如直接代入计算出y1与y2,并比较大小正确参照给分)
-
科目: 来源: 题型:
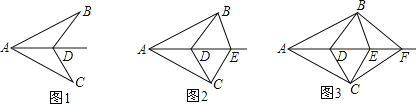
查看答案和解析>>【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
-
科目: 来源: 题型:
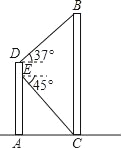
查看答案和解析>>【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连接BD.

(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
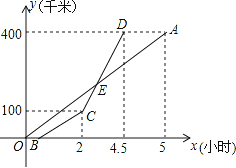
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1) 3x-2(x-1)= 2- 3(5-2x)
(2)
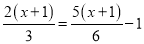
(3)
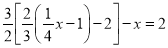
(4)
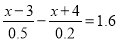
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_________;
(2)仔细观察,在图2中“8字形”的个数_________个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角,其他条件不变,试问∠P与∠D,∠B之间存在着怎样的数量关系(直接写出结论即可)
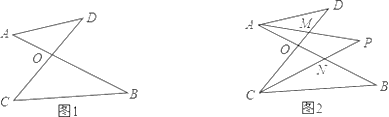
相关试题

