【题目】某校墙边有两根木杆.
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
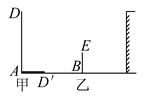
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
参考答案:
【答案】(1)画图见解析;(2)见解析;(3)有,△ADD′与△BEE′相似.
【解析】试题分析:(1)连接甲木杆影子的顶端和甲木杆的顶端DD′就是光线的位置,同时太阳光线是平行的,经过点E作DD′的平行线交AB于点E′即可画出乙木杆的影子;
(2)平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚即可;
(3)利用相似三角形的判定找出相似三角形.
试题解析:
解:(1)如答图1,连接DD′,过E点作直线DD′的平行线,交AD′所在直线于E′,则BE′为乙木杆的影子;
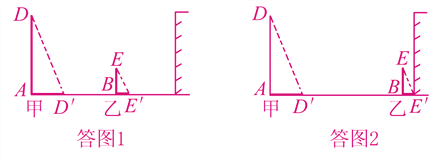
(2)如答图2,平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚;
(3)有,△ADD′与△BEE′相似.
∵DD′∥EE′,
∴∠DD′A=∠EE′B ,
又∵∠DAD′=∠EBE′,
∴△ADD′∽△BEE′(两角对应相等,两三角形相似).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料并填空:
①(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣ ,反过来,得1﹣
,反过来,得1﹣ =(1﹣
=(1﹣ )(1+
)(1+ )=
)= ×
× ;
;②(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣ ,反过来,得1﹣
,反过来,得1﹣ =(1﹣
=(1﹣ )(1+
)(1+ )= × ;
)= × ;③(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣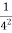 ,反过来,得1﹣
,反过来,得1﹣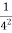 = =
= = ;
;利用上面的材料中的方法和结论计算下题:
(1﹣
 )(1﹣
)(1﹣ )(1﹣
)(1﹣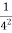 )……(1﹣
)……(1﹣ )(1﹣
)(1﹣ )(1﹣
)(1﹣ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
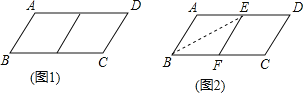
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行了如下操作:如图,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(2)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;

(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
相关试题

