【题目】如图,已知![]() 是△
是△![]() 的外角
的外角![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交△
交△![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]() ,
, ![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,若
,若![]() 是△
是△![]() 外接圆的直径,
外接圆的直径, ![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)由四边形AFBC内接于圆可证得∠DAC=∠FBC;由AD平分∠EAC可得∠EAD=∠DAC,结合∠EAD=∠FAB,∠FAB=∠FCB,可得∠FCB=∠DAC,从而可得结论:∠FBC=∠FCB;
(2)由已知条件易证△ABF∽△BDF,由此可得: ![]() 即
即![]() ,从而可解得
,从而可解得![]() ;
; ![]() ,
, ![]() 可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=
可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=![]() ,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
试题解析:
(![]() )∵四边形
)∵四边形![]() 内接于圆,
内接于圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是△
是△![]() 的外角
的外角![]() 平分线,
平分线,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(![]() )由(
)由(![]() )得
)得![]() ,
,
又∵![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∴BD=![]() ,
,
又∵∠D=∠D,
∴△DBF∽△DAC,
∴![]() ,
,
∴![]() CD=24,解得:CD=
CD=24,解得:CD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点 在边
在边 上移动(点
上移动(点 不与点
不与点 ,
,  重合),满足
重合),满足 ,且点
,且点 、
、 分别在边
分别在边 、
、 上.
上.(
 )求证:
)求证:  .
.(
 )当点
)当点 移动到
移动到 的中点时,求证:
的中点时,求证:  平分
平分 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】模型建立:
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.

求证:△BEC≌△CDA.
模型应用:
(2)已知直线l1:y=
 x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.
x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.(3)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为
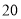 元/个的计算器,其销售量
元/个的计算器,其销售量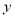 (万个)与销售价格
(万个)与销售价格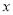 (元/个)的变化如下表:
(元/个)的变化如下表:价格
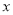 (元/个)
(元/个)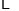
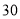
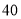
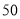
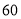
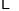
销售量
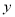 (万个)
(万个)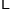
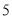
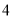
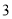
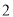
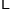
同时,销售过程中的其他开支(不含造价)总计
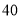 万元.
万元.(
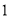 )观察并分析表中的
)观察并分析表中的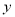 与
与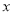 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出
之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出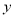 (万个)与
(万个)与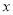 (元/个)的函数解析式.
(元/个)的函数解析式.(
 )求出该公司销售这种计算器的净得利润
)求出该公司销售这种计算器的净得利润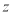 (万个)与销售价格
(万个)与销售价格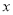 (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(
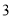 )该公司要求净得利润不能低于
)该公司要求净得利润不能低于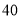 万元,请写出销售价格
万元,请写出销售价格 (元/个)的取值范围.
(元/个)的取值范围.
相关试题

