【题目】已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;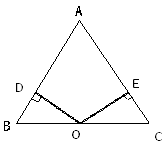
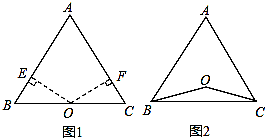
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
参考答案:
【答案】
(1)解:证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL), (1)由HL判断出Rt△OEB≌Rt△OFC ,根据全等三角形对应角相等得出∠ABC=∠ACB ,根据等角等等边得出AB=AC ;
∴∠ABC=∠ACB,
∴AB=AC
(2)证明:过点O分别作OD⊥AB于D,OE⊥AC于E,
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如图)
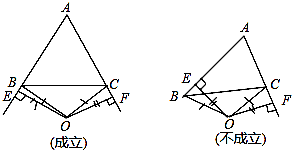
【解析】 (1)由HL判断出Rt△OEB≌Rt△OFC ,根据全等三角形对应角相等得出∠ABC=∠ACB ,根据等角等等边得出AB=AC ;
(2)过点O分别作OD⊥AB于D,EF⊥AC于E,根据HL判断出Rt△ODB≌Rt△OEC ,根据全等三角形的性质得出∠OBD=∠OCE,由根据等边对等角得出∠OBC=∠OCB,从而得出∠ABC=∠ACB,根据等角对等边得出AB=AC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如图)
【考点精析】通过灵活运用角平分线的性质定理和线段垂直平分线的性质,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列正多边形材料中,不能单独用来铺满地面的是( ).
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2x+3y﹣4=0,求4x8y的值.
-
科目: 来源: 题型:
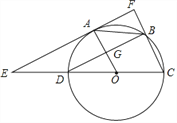
查看答案和解析>>【题目】如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形。过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)求证:EF是⊙O的切线;
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
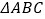 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,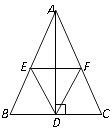
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的面积为(4a2-6ab+2a),如果它的长为2a,则它的宽为_____.
相关试题

