【题目】在平面宜角坐标系xOy中,直线y=![]() x+4与x轴,y轴交于点A,B.第一象限内有一点P(m,n),正实数m,n满足4m+3n=12
x+4与x轴,y轴交于点A,B.第一象限内有一点P(m,n),正实数m,n满足4m+3n=12
(1)连接AP,PO,△APO的面积能否达到7个平方单位?为什么?
(2)射线AP平分∠BAO时,求代数式5m+n的值;
(3)若点A′与点A关于y轴对称,点C在x轴上,且2∠CBO+∠PA′O=90°,小慧演算后发现△ACP的面积不可能达到7个平方单位.请分析并评价“小薏发现”.
参考答案:
【答案】(1)不能;(2)9;(3)见解析.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A的坐标,由△APO的面积等于7个平方单位可求出n值,代入4m+3n=12中可求出m值为负,由此可得出△APO的面积不能达到7个平方单位;
(2)设AP与y轴交于点E,过点E作EF⊥AB于点F,利用面积法及角平分线的性质可求出点E的坐标,由点A,E的坐标,利用待定系数法可求出直线AP的解析式,由m,n满足4m+3n=12可得出直线BP的解析式,联立直线AP,BP的解析式成方程组,通过解方程组可求出m,n的值,再将其代入5m+n中即可得出结论;
(3)当点C在x轴正半轴时,由2∠CBO+∠PA′O=90°可得出BC平分∠OBA′,同(2)可求出C的坐标,进而可求出AC的长,利用三角形的面积公式可求出△ACB的面积,由该值大于7可得出:存在点P,使得△ACP的面积等于7个平方单位;当点C在x轴正半轴时,利用对称可得出点C的坐标,进而可求出AC的长,利用三角形的面积公式可求出△ACB的面积,由该值小于7可得出:此种情况下,△ACP的面积不可能达到7个平方单位.综上,此题得解.
(1)△APO的面积不能达到7个平方单位,理由如下:
当y=0时,![]() x+4=0,解得:x=-3,
x+4=0,解得:x=-3,
∴点A的坐标为(-3,0).
∴S△APO=![]() OAn=7,即
OAn=7,即![]() n=7,
n=7,
∴n=![]() .
.
又∵4m+3n=12,
∴m=-2,这与m为正实数矛盾,
∴△APO的面积不能达到7个平方单位.如图1,
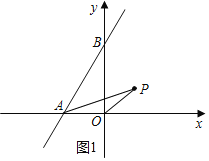
(2)设AP与y轴交于点E,过点E作EF⊥AB于点F,如图2所示.
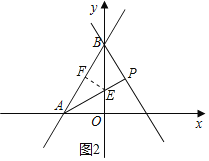
当x=0时,y=![]() x+4=4,
x+4=4,
∴点B的坐标为(0,4),
∴AB=![]() =5.
=5.
∵AP平分∠BAO,
∴EO=EF.
∵S△ABE=![]() BEOA=
BEOA=![]() ABEF,S△AOE=
ABEF,S△AOE=![]() EOOA,
EOOA,
∴![]() ,即
,即![]() ,
,
∴EO=![]() ,
,
∴点E的坐标为(0,![]() ).
).
设直线AP的解析式为y=kx+b(k≠0),
将A(-3,0),E(0,![]() )代入y=kx+b,得:
)代入y=kx+b,得:
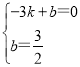 ,解得:
,解得:![]() ,
,
∴直线AP的解析式为y=![]() x+
x+![]() .
.
∵点P的坐标为(m,n),m,n满足4m+3n=12,
∴点P在直线y=-![]() x+4上.
x+4上.
联立直线AP,BP的解析式成方程组,得:
 ,
,
解得: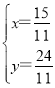 ,
,
∴m=![]() ,n=
,n=![]() ,
,
∴5m+n=9.
(3)“小薏发现”不对,理由如下:
依照题意,画出图形,如图3所示.
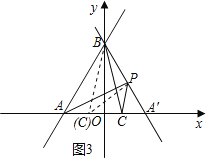
∵2∠CBO+∠PA′O=90°,∠OBA′+∠PA′O=90°,
∴∠OBA′=2∠CBO.
∵点A′与点A关于y轴对称,
∴点A′的坐标为(3,0),点P在线段BA′上.
当点C在x轴正半轴时,BC平分∠OBA′,
同(2)可得出:![]() ,即
,即![]() ,
,
∴OC=![]() ,
,
∴点C的坐标为(![]() ,0),
,0),
∴AC=![]() .
.
∵S△ACB=![]() ACOB=
ACOB=![]() ×
×![]() ×4=
×4=![]() >7,
>7,
∴不存在点P,使得△ACP的面积等于7个平方单位;
当点C在x轴负半轴时,点C的坐标为(-![]() ,0),
,0),
∴AC=![]() .
.
∵S△ACB=![]() ACOB=
ACOB=![]() ×
×![]() ×4=
×4=![]() <7,
<7,
∴此种情况下,△ACP的面积不可能达到7个平方单位.
综上所述:“小薏发现”不正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
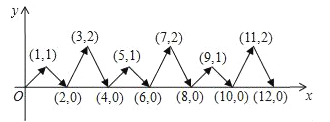
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从顶点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2010次运动后,动点P的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石子摆成的小房子,请根据图中的信息完成下列的问题:

(1)填写下表:
图形编号
①
②
③
④
……
图中石子的总数
……
(2)第30个图形需要用 颗石子;
(3)如果继续摆放下去,那么第
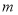 个图案要用 颗石子;
个图案要用 颗石子;(4)该同学准备用300颗石子来摆放第
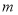 个图案,摆放成完整的图案后,第
个图案,摆放成完整的图案后,第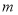 个图案 能否刚好用完这300颗石子?如果可以,求出
个图案 能否刚好用完这300颗石子?如果可以,求出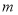 的值,如果不能,求出
的值,如果不能,求出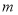 的最大值以及至少还剩余多少颗石子.
的最大值以及至少还剩余多少颗石子. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
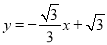 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.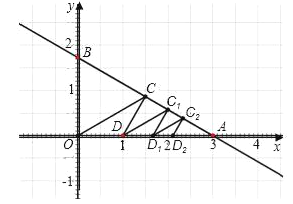
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图中正方形四个顶点所标的数字规律,可知数2019应标在( )

A. 第505个正方形的左上角B. 第505个正方形的右下角
C. 第504个正方形的左上角D. 第504个正方形的右下角
-
科目: 来源: 题型:
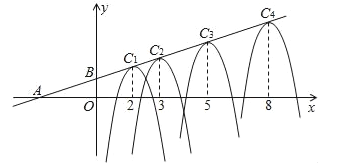
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(﹣3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C2的顶点坐标为_____;抛物线C8的顶点坐标为_____.
相关试题

