【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.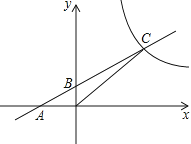
参考答案:
【答案】解:设一次函数的解析式为y=kx+b,
把A(﹣2,0),B(0,1)代入得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式为y= ![]() x+1;
x+1;
设反比例函数的解析式为y= ![]() ,
,
把C(4,n)代入得:n=3,
∴C(4,3),
把C(4,3)代入y= ![]() 得:m=3×4=12,
得:m=3×4=12,
∴反比例函数的解析式为y= ![]() .
.
【解析】设一次函数的解析式为y=kx+b,把A(﹣2,0),B(0,1)代入得出方程组,解方程组即可;求出点C的坐标,设反比例函数的解析式为y= ![]() ,把C(4,3)代入y=
,把C(4,3)代入y= ![]() 求出m即可.本题考查了用待定系数法求出函数的解析式,一次函数和和反比例函数的交点问题,函数的图象的应用,主要考查学生的观察图形的能力和计算能力.
求出m即可.本题考查了用待定系数法求出函数的解析式,一次函数和和反比例函数的交点问题,函数的图象的应用,主要考查学生的观察图形的能力和计算能力.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
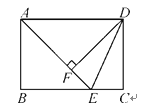
查看答案和解析>>【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣14+
 sin60°+(
sin60°+(  )﹣2﹣(
)﹣2﹣(  )0 .
)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b、c满足(b﹣3)2+|c+4|=0,且a,b,c分别是点A,B,C在数轴上对应的数.
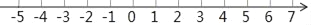
(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校团委组织了有奖征文活动,并设立了一、二、三等奖,根据设奖情况买了50 件奖品,其二等奖奖品的件数比一等奖奖品的件数的2 倍少10, 各种奖品的单价如下表所示:

如果计划一等奖奖品买x件,买5 件奖品的总数是y元.
(1)先填表,再用含x的代数式表示y并化简;
(2)若一等奖奖品买10件,则共花费多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
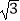 =1.732,
=1.732,  =1.414)
=1.414)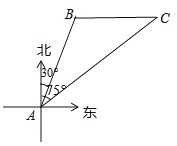
相关试题

