【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a,b,c分别满足:-(a-4)2≥0,c=![]() +
+![]() +8.
+8.
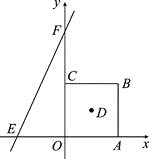
(1)直线y=bx+c的解析式为________;正方形OABC的对角线的交点D的坐标为________;
(2)若正方形OABC沿x轴负方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,在备用图中画图分析,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)y=2x+8, D(2,2);(2)t=5;(3)![]() .
.
【解析】
(1)由已知条件易得:a=4,b=2,c=8,由此即可得到直线EF的解析式为:y=2x+8,点B的坐标为(4,4),结合点D是正方形OABC对角线的交点可得点D的坐标为(2,2);
(2)由点D是正方形OABC的对称中心可知,当点D落在直线EF上时,直线EF平分正方形OABC的面积,由已知条件设当点D落在EF上时的坐标为(2-t,2),将此坐标代入直线EF的解析式即可求得对应的t的值;
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,结合已知条件易证四边形PNCG是正方形,四边形PGBQ是矩形,四边形OHGC是矩形,PH=PQ,∠OPH=∠MPQ,由此证得△OPH≌△MPQ,从而可得QM=OH=CG=GP=BQ=![]() BM,结合PC=
BM,结合PC=![]() GP即可得到PC=
GP即可得到PC=![]() BM,由此即可得到
BM,由此即可得到![]() .
.
(1)∵![]() ,
,
∴![]() 且
且![]() ,
,
∴b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8;
∵![]() ,
,
∴![]() ,
,
∴a=4,
∴OA=AB=4,
∴点B的坐标为(4,4),
∴点D是正方形OABC对角线的交点,
∴点D是线段OB的交点,
∴点D的坐标为(2,2);
(2)存在,理由如下:
如图1,∵点D是正方形OABC的对角线的交点,
∴过点D的直线都能把正方形AOCB的面积分成相等的两部分,
∴当正方形AOCB平移到直线EF过D点时,直线正好平分正方形的面积,
设平移后的D点坐标为(2-t,2),
把它代入直线y=2x+8,2(2-t)+8=2,
解得:t=5;
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中: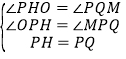
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,四边形AOBC是正方形,
∴易得四边形CNPG为正方形,四边形PGBQ是矩形,四边形OHGC是矩形,
∴PG=BQ=CG=OH=QM,
∴PG=![]() BM,
BM,
∵在正方形CNPG中,PC=![]() PG,
PG,
∴PC=![]() BM,
BM,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为
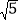 、
、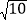 、
、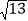 ,求△ABC的面积.
,求△ABC的面积.小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:

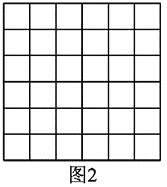
(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为
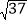 、2
、2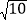 、
、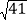 的格点△DEF.
的格点△DEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2
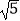 ,sin∠AOC=
,sin∠AOC= 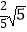 ,反比例函数y=
,反比例函数y= 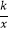 的图象经过点C以及边AB的中点D.
的图象经过点C以及边AB的中点D. 
(1)求这个反比例函数的解析式;
(2)四边形OABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).

(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
-
科目: 来源: 题型:
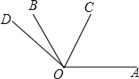
查看答案和解析>>【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
相关试题

