【题目】如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,试求:
(1)AD的长度;
(2)△ACE和△ABE的周长的差.
参考答案:
【答案】(1)AD的长度为![]() cm;(2)△ACE和△ABE的周长的差是3cm.
cm;(2)△ACE和△ABE的周长的差是3cm.
【解析】
(1)利用直角三角形的面积法来求线段AD的长度;
(2)由于AE是中线,那么BE=CE,再表示△ACE的周长和△ABE的周长,化简可得△ACE的周长﹣△ABE的周长=AC﹣AB即可.
解:(1)∵∠BAC=90°,AD是边BC上的高,
∴S△ACB=![]() ABAC=
ABAC=![]() BCAD,
BCAD,
∵AB=9cm,AC=12cm,BC=15cm,
∴AD=![]() =
=![]() =
=![]() (cm),
(cm),
即AD的长度为![]() cm;
cm;
(2)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=12﹣9=3(cm),
即△ACE和△ABE的周长的差是3cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.
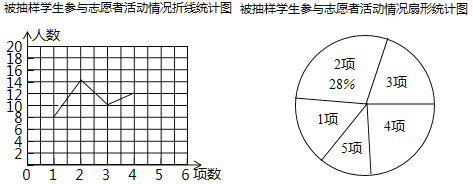
(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E.若线段AE=2,则四边形ABCD的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型
乙型
价格(元/台)
a
b
有效半径(米/台)
150
100
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
相关试题

