【题目】如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G. 
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ABC+∠BAD=180°.
又∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB+∠ACE=180°,
∴∠BAD=∠ACE.
∵CE=BC,
∴CE=AD,
在△ABE和△CEA中, 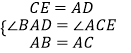 ,
,
∴△ADB≌△CEA(SAS)
(2)解:∵△ADB≌△CEA,
∴AE=BD=9.
∵AD∥BC,
∴△ADF∽△EBF.
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
∴AF=3
【解析】(1)由平行四边形的性质得出AD=BC,∠ABC+∠BAD=180°,由等腰三角形的性质得出∠ABC=∠ACB.证出∠BAD=∠ACE,CE=AD,由SAS证明△ADB≌△CEA即可;(2)由全等三角形的性质得出AE=BD=6,由平行线得出△ADF∽△EBF,得出对应边成比例,即可得出结果.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
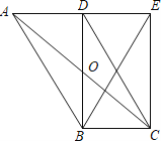
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(1)将两个矩形叠合成如图10,求证:四边形ABCD是菱形;
(2)若菱形ABCD的周长为20,BE=3,求矩形BEDG的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,任意四边形ABCD,对角线AC、BD交于O点,过各顶点分别作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH的形状会有哪些变化?完成以下题目:
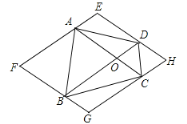
(1)①当ABCD为任意四边形时,四边形EFGH为___________;
②当四边形ABCD为矩形时,四边形EFGH为___________;
③当四边形ABCD为菱形时,四边形EFGH为___________;
④当四边形ABCD为正方形时,四边形EFGH为___________;
(2)请对(1)中①③你所写的结论进行证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图所示,试根据图象,回答下列问题:
(1)慢车比快车早出发______小时,快车追上慢车时行驶了_____千米,快车比慢车早______小时到达B地;
(2)求慢车、快车的速度;
(3)快车追上慢车需几个小时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形
 中,在
中,在 边上取两点
边上取两点 、
、 ,使
,使 .若
.若 ,
, ,
, , 则以
, 则以 ,
, ,
, 为边长的三角形的形状为( )
为边长的三角形的形状为( )
A.锐角三角形B.直角三角形C.钝角三角形D.随
 ,
, ,
, 的值而定
的值而定
相关试题

