【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=ABAE.
求证:DE是⊙O的切线.
参考答案:
【答案】证明:连接DC,DO并延长交⊙O于F,连接AF. 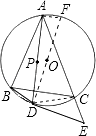
∵P点为△ABC的内心,
∴∠BAD=∠DAE,
又∵AD2=ABAE,即 ![]() =
= ![]() ,
,
∴△BAD∽△DAE,
∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
【解析】连接DC、AF,连接DO并延长交圆O于点F,先证△BAD∽△DAE,得到∠ADB=∠E,再由平行线的性质可证∠FDE=90°可得.解答此题的关键是作出辅助线,证出△BAD∽△DAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.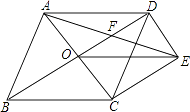
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2 , 后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
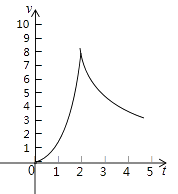
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使S△QAM= S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
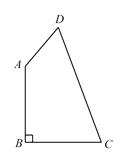
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
相关试题

