【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P。
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试写出∠PAC,∠APB,∠PBD之间的关系,并说明理由。(图3只写结论,不写理由)



参考答案:
【答案】(1)当P点在C、D之间运动时,∠APB=∠PAC+∠PBD(2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.(3)∠PAC=∠PBD+∠APB
【解析】分析:(1)当P点在C、D之间运动时,首先过点P作,由,可得,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动时,由直线,根据两直线平行,同位角相等与三角形外角的性质,即可求得: ∠PBD=∠PAC+∠APB.
本题解析: 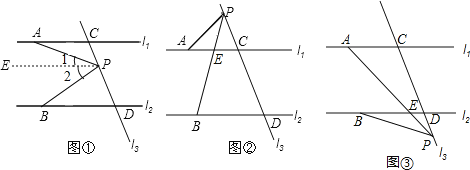
(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图②,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
(3)如图(3),当点P在C、D两点的外侧运动,且在![]() 下方时,∠PAC=∠PBD+∠APB.
下方时,∠PAC=∠PBD+∠APB.
理由如下:理由如下:
∵![]() ∥
∥![]() ,
,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用电基本价格为每度0.4元,若每月用电量超过a度,超过部分按每度0.6元收费,若某户居民九月份用电84度,共交电费40.4元,则a为( )
A. 50度 B. 55度 C. 60度 D. 65度
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“一个三角形中至多有一个角不小于90°”时,应假设( )
A. 一个三角形中至少有两个角不小于 90°
B. 一个三角形中至多有一个角不小于 90°
C. 一个三角形中至少有一个角不小于 90°
D. 一个三角形中没有一个角不小于 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
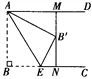
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
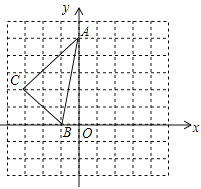
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂一月份生产某机器100台,计划二、三月份共生产280台.设二、三月份每月的平均增长率为x,根据题意列出的方程是( )
A.100(1+x)2=280
B.100(1+x)+100(1+x)2=280
C.100(1﹣x)2=280
D.100+100(1+x)+100(1+x)2=280 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地市话的收费标准是:(1)通话时间在3分钟以内(含3分钟)话费为0.22元;(2)通话时间超过3分钟时,超过部分按每分钟0.11元计,小王某次的市话费为0.77元,则小王的通话时间为____分钟.
相关试题

