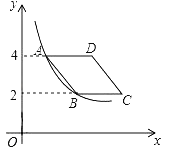
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为______.
,则k的值为______.
参考答案:
【答案】4
【解析】
过点A作x轴的垂线,交CB的延长线于点E,根据A,B两点的纵坐标分别为4,2,可得出横坐标,即可求得AE,BE的长,根据菱形的面积为![]() ,求得AE的长,在Rt△AEB中,即可得出k的值.
,求得AE的长,在Rt△AEB中,即可得出k的值.
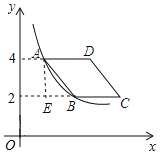
解:过点A作x轴的垂线,交CB的延长线于点E,
∵A,B两点在反比例函数![]() (x>0)的图象,且纵坐标分别为4,2,
(x>0)的图象,且纵坐标分别为4,2,
∴A(![]() ,4),B(
,4),B(![]() ,2),
,2),
∴AE=2,![]() ,
,
∵菱形ABCD的面积为![]() ,
,
∴BC×AE=![]() ,即BC=
,即BC=![]() ,
,
∴AB=BC=![]() ,
,
在Rt△AEB中,![]() ,
,
∴![]() ,
,
∴k=4.
故答案为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=
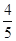 ,反比例函数y=
,反比例函数y= 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.(1)求反比例函数解析式;
(2)若函数y=3x与y=
 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.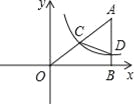
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G, FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED; ②△DFG ≌△DCG;③△FHB∽△EAD;④tan∠GEB=
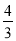 ;⑤S△BFG=2.4.其中正确的个数是( )
;⑤S△BFG=2.4.其中正确的个数是( )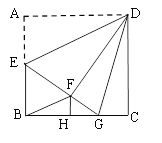
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度
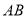 ,他站在距离教学楼底部
,他站在距离教学楼底部 处6米远的地面
处6米远的地面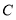 处,测得宣传牌的底部
处,测得宣传牌的底部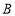 的仰角为
的仰角为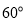 ,同时测得教学楼窗户
,同时测得教学楼窗户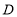 处的仰角为
处的仰角为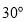 (
(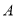 、
、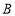 、
、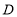 、
、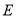 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度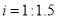 的斜坡从
的斜坡从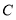 走到
走到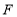 处,此时
处,此时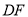 正好与地面
正好与地面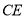 平行.
平行.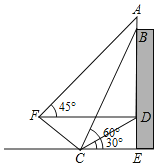
(1)求点
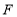 到直线
到直线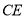 的距离(结果保留根号);
的距离(结果保留根号);(2)若小明在
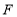 处又测得宣传牌顶部
处又测得宣传牌顶部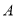 的仰角为
的仰角为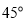 ,求宣传牌的高度
,求宣传牌的高度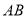 (结果精确到0.1米,
(结果精确到0.1米,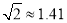 ,
,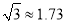 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别
学习时间x(h)
人数(人)
A
2.5<x≤3
40
B
3<x≤3.5
170
C
3.5<x≤4
350
D
4<x≤4.5
E
4.5<x≤5
90
F
5小时以上
50
表1
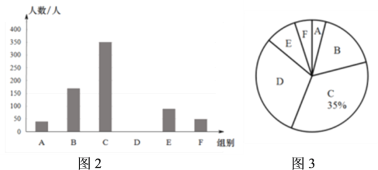
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)图3中D组对应的角度是 ,并补全图2 条形统计图.
(3)若某市有初中学生2.8万人,请估计每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

相关试题

