搜索
【题目】二次函数y＝（x﹣2）2当2﹣a≤x≤4﹣a，最小值为4，则a的值为_____．
参考答案：
【答案】4或﹣2．
【解析】
根据二次函数图象的开口方向知道，当x＝0或x＝4时，函数值的最小值是4，结合函数图象得到当x≤0或x≥4时，符合题意．
解：∵二次函数y＝（x﹣2）2当2﹣a≤x≤4﹣a，最小值为4，
∴当x＝0或x＝4时，y最小值＝4．
如图，当x≤0或x≥4时，y最小值＝4．
∵2﹣a≤x≤4﹣a，
∴a＝4或a＝﹣2．
故答案是：4或﹣2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若线段AB∥y轴，且AB＝3，点A的坐标为（2，1），现将线段AB先向左平移1个单位，再向下平移两个单位，则平移后B点的坐标为（ ）
A.（1，2）B.（1，﹣4）
C.（﹣1，﹣1）或（5，﹣1）D.（1，2）或（1，﹣4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果（m﹣1）x2+2x﹣3＝0是一元二次方程，则m的取值范围为_____．
-
科目： 来源： 题型：
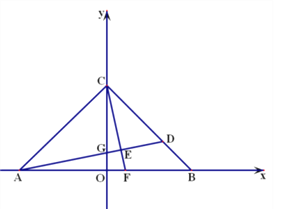
查看答案和解析>>【题目】如图，在平面直角坐标系中，OA=OB=OC=6，过点A的直线AD交BC于点D，交y轴与点G，△ABD的面积为△ABC面积的
.(1)直接写出点D的坐标;
(2)过点C作CE⊥AD，交AB交于F，垂足为E．
①求证：OF=OG；（3分） ②求点F的坐标．
(3)在(2)的条件下，在第一象限内是否存在点P，使△CFP为等腰直角三角形，若存在，直接写出点P坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的平面直角坐标系中表示下面各点:
A（0，3）；B（1，-3）；C（3，-5）；D（-3，-5）；E（3，5）；F（5，7）；G（5，0）
（1）A点到原点O的距离是 。
（2）将点C向
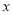轴的负方向平移6个单位，它与点 重合。（3）连接CE，则直线CE与
轴是什么关系？（4）点F分别到
、
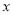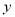轴的距离是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知OM平分∠AOC，ON平分∠BOC，∠AOB=90°，∠BOC=30°．
求：（1）∠AOC的度数；
（2）∠MON的度数．
-
科目： 来源： 题型：
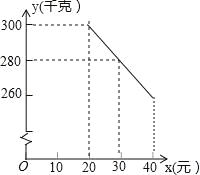
查看答案和解析>>【题目】(2016云南省第22题)草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量y（千克）与销售单价x（元）符合一次函数关系，如图是y与x的函数关系图象．
（1）求y与x的函数解析式（也称关系式）
（2）设该水果销售店试销草莓获得的利润为W元，求W的最大值．
相关试题
