【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.

(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
参考答案:
【答案】(1)![]()
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
【解析】
试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为![]() 。
。
又∵二次函数图象经过原点(0,0),∴![]() ,解得
,解得![]() 。
。
∴二次函数的关系式为![]() ,即
,即![]() 。(2分)
。(2分)
(2)设直线OA的解析式为![]() ,将A(6,-3)代入得
,将A(6,-3)代入得![]() ,解得
,解得![]() 。
。
∴直线OA的解析式为![]() 。
。
把x=4代入![]() 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。
又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴![]() 。(3分)
。(3分)
(3)①证明:过点A作AH⊥![]() 于点H,,
于点H,,![]() 与x轴交于点D。则
与x轴交于点D。则
设A(![]() ),
),
则直线OA的解析式为 。
。
则M(![]() ),N(
),N(![]() ),H(
),H(![]() )。
)。
∴OD=4,ND=![]() ,HA=
,HA=![]() ,NH=
,NH=![]() 。
。
∴ 。
。
∴![]()
![]() 。∴∠AM=∠ONM。(2分)
。∴∠AM=∠ONM。(2分)
②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则![]() 。
。
∵![]() ,
,
∴![]() 。
。
整理,得![]() ,解得
,解得![]() ,
,![]() 。
。
∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴![]() 。
。
∵OD=4,MD=![]() ,ND=
,ND=![]() ,∴
,∴![]() 。
。
整理,得![]() ,解得
,解得![]() 。
。
∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴![]() 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等
的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转
动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区
域为止).

【1】请你用画树状图或列表格的方法求出|m+n|>1的概率
【2】直接写出点(m,n)落在函数y=- 图象上的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1﹣8这8个整数,现提供统计图的部分信息如图,请解答下列问题:

(1)根据统计图,求这50名工人加工出的合格品数的中位数;
(2)写出这50名工人加工出的合格品数的众数的可能取值;
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并解决问题:有趣的勾股数组
定义:一般地,若三角形三边长
 ,
, ,
, 都是正整数,且满足
都是正整数,且满足 ,那么数组
,那么数组 称为勾股数组.
称为勾股数组.关于勾股数组的研究我国历史上有过非常辉煌的成就,根据我国古代数学书《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三,股修四,径隅五”(古人把较短的直角边称为勾,较长直角边称为股,而斜边则成称为弦),即知道了勾股数组
 ,后来人们发现并证明了勾股定理.
,后来人们发现并证明了勾股定理.公元263年魏朝刘徽注《九章算术》,文中除提到勾股数组
 以外,还提到
以外,还提到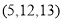 ,
, ,
, ,
, 等勾股数组.
等勾股数组.设
 ,
, 是两个正整数,且
是两个正整数,且 ,三角形三边长
,三角形三边长 ,
, ,
, 都是正整数.
都是正整数.下表中的
 ,
, ,
, 可以组成一些有规律的勾股数组
可以组成一些有规律的勾股数组 :
:




2
1
3
4
5
3
2
5
12
13
4
1
15
8
17
4
3
7
24
25
5
2
21
20
29
5
4
9
40
41
6
1
35
12
37
6
5
11
60
61
7
2
45
28
53
7
4
33
56
65
7
6
13
84
85
请你仔细观察这个表格,解答下列问题:
(1)表中
 和
和 ,
, 的等量关系式是________;
的等量关系式是________;(2)表中的勾股数组用只含
 ,
, 的代数式表示为________;
的代数式表示为________;(3)小明通过研究表中数据发现:若勾股数组中,弦与股的差为1,则勾股数的形式可表述为
 (
( ,
, 为正整数),请你用含
为正整数),请你用含 的代数式表示
的代数式表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往
 ,
, ,
, 三地销售,要求运往
三地销售,要求运往 地的袋数是运往
地的袋数是运往 地袋数的3倍,各地的运费如下表所示:
地袋数的3倍,各地的运费如下表所示:运往地
 地
地 地
地 地
地运费(元/袋)
20
10
15

(1)设运往
 地的小米为
地的小米为 (袋),总运费为
(袋),总运费为 (元),试写出
(元),试写出 与
与 的函数关系式;
的函数关系式;(2)若总运费不超过14000元,最多可运往
 地多少袋小米?
地多少袋小米? -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境:如图1,在正方形
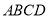 中,点
中,点 是对角线
是对角线 上的一点,点
上的一点,点 在
在 的延长线上,且
的延长线上,且 ,
, 交
交 于点
于点 .问题解决:
.问题解决:
(1)求证:
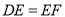 ;
;(2)求
 的度数;
的度数;探索发现:
(3)如图2,若点
 在边
在边 上,且
上,且 ,求
,求 的度数.
的度数.
相关试题

