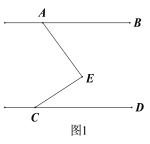
【题目】如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿射线CD平移至FG.
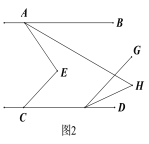
①如图2,若∠AEC=90°,FH平分∠DFG,求∠AHF的度数;
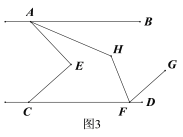
②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
参考答案:
【答案】(1)见解析;(2)①45°;②∠AHF=90°+![]() ∠AEC(或2∠AHF-∠AEC=180°),理由见解析.
∠AEC(或2∠AHF-∠AEC=180°),理由见解析.
【解析】
(1)过E作EF∥AB,可得∠A=∠AEN,利用平行于同一条直线的两直线平行得到EN与CD平行,再得到一对内错角相等,进而得出答案;
(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数,再由∠AEC=90°,根据角的关系易得∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及(1)中结论即可得到∠AHF与∠AEC的数量关系.
(1)如图1,过点E作直线EN∥AB,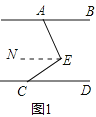
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAE+∠ECD;
(2)∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°-x,
如图2,过点H作l∥AB,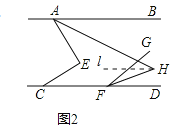
易证∠AHF=∠BAH+∠DFH=45°-x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°-x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,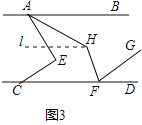
易证∠AHF-y+∠CFH=180°,
即∠AHF-y+90°-x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+![]() ∠AEC.(或2∠AHF-∠AEC=180°.)
∠AEC.(或2∠AHF-∠AEC=180°.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 坐标为
坐标为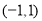 ,点
,点 坐标为
坐标为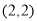 ,正方形
,正方形 沿
沿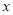 轴向左平移,若与正方形
轴向左平移,若与正方形 重叠部分的面积为
重叠部分的面积为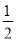 平方单位,则
平方单位,则 点移动后的坐标是_______.
点移动后的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”,他的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数,例如:(a+b)2=a2+2ab+b2展开式中的系数1,2,1恰好对应图中第三行的数字;(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1,3,3,1恰好对应图中第四行的数字…….请认真观察此图,根据前面各式的规律,写出(a+b)6的展开式:(a+b)6=____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅,1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅,1个小餐厅分别可供多少名 就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
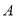 在
在 的一边
的一边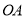 上,按要求画图并填空:
上,按要求画图并填空:(1)过点
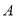 画直线
画直线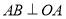 ,与
,与 的另一边相交于点
的另一边相交于点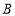 ;
;(2)过点
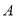 画
画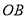 的垂线
的垂线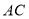 ,垂足为点
,垂足为点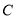 ;
;(3)过点
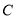 画直线
画直线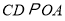 ,交直线
,交直线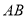 于点
于点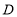 ;
;(4)直接写出
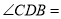 _____
_____ ;
;(5)如果
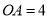 ,
,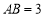 ,
,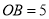 ,那么点
,那么点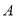 到直线
到直线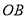 的距离为_______.
的距离为_______.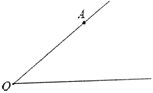
-
科目: 来源: 题型:
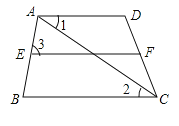
查看答案和解析>>【题目】完成下面的证明过程:
已知:如图,
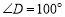 ,
,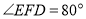 ,
,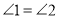 .
.求证:
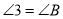 .
.
证明:∵
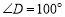 ,
,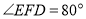 (已知)
(已知)∴
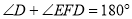 .
.∴
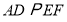 ,( )
,( )又∵
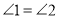 ,(已知)
,(已知)∴______
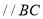 ,(内错角相等,两直线平行)
,(内错角相等,两直线平行)∴
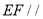 _______,( )
_______,( )∴
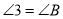 .( )
.( ) -
科目: 来源: 题型:
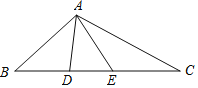
查看答案和解析>>【题目】如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,则∠BAC的度数是( )
A.
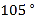 B.
B. 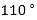 C.
C. 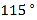 D.
D. 
相关试题

