【题目】数轴上表示数![]() 的点与原点的距离叫做数
的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]() .数轴上表示数
.数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离记作
的点的距离记作![]() ,如
,如![]() 表示数轴上表示数3的点与表示数5的点的距离,
表示数轴上表示数3的点与表示数5的点的距离,![]() 表示数轴上表示数3的点与表示数-5的点的距离,
表示数轴上表示数3的点与表示数-5的点的距离,![]() 表示数轴上表示数
表示数轴上表示数![]() 的点与表示数3的点的距离.
的点与表示数3的点的距离.
![]()
根据以上材料回答下列问题:(将结果直接填写在答题卡相应位置,不写过程)
(1)若![]() ,则
,则![]() ________,若
________,若![]() ,则
,则![]() ___________;
___________;
(2)若![]() ,则
,则![]() 能取到的最小值是_________,最大值是_________;
能取到的最小值是_________,最大值是_________;
(3)关于![]() 的式子
的式子![]() 的取值范围是_________.
的取值范围是_________.
参考答案:
【答案】(1)0;0.5;(2)-1,2;(3)![]()
![]()
【解析】
(1)数轴上与表示1的点和表示-1的点距离相等的点所表示的数为0,数轴上与表示2的点和表示-1的点距离相等的点所表示的数为0.5,即可得到结论;
(2)数轴上表示2的点和表示-1的点的距离是3,故在此范围内x的最小取值是-1,最大取值是2,即可得解;
(3)由题意知|![]() 表示数x到2和-1的距离之和,当数x在两数之间时式子取得最小值,由此可得
表示数x到2和-1的距离之和,当数x在两数之间时式子取得最小值,由此可得![]() 的取值范围.
的取值范围.
(1)根据数轴上与表示1的点和表示-1的点距离相等的点所表示的数为0,
可得:若![]() ,则x=0;
,则x=0;
根据数轴上与表示2的点和表示-1的点距离相等的点所表示的数为0.5,
可得:若![]() ,则x=0.5;
,则x=0.5;
故答案为:0;0.5;
(2)∵数轴上表示2的点和表示-1的点的距离是3,
即当x![]() 时,
时,![]() ,
,
∴x的最小取值是-1,最大取值是2,
故答案为:-1,2;
(3)∵![]() 表示数x到2和-1的距离之和,
表示数x到2和-1的距离之和,
∴当![]() 时,
时,![]() ,当x>2或x<-1时,
,当x>2或x<-1时,![]() ,
,
∴![]() .
.
故答案为:![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
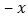 ,
,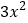 ,
,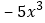 ,
,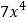 ,…
,…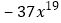 ,
,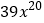 ,…写出第
,…写出第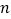 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.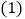 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?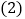 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?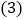 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第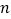 个单项式是什么?
个单项式是什么?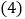 请你根据猜想,请写出第
请你根据猜想,请写出第 个,第
个,第 个单项式.
个单项式. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,国家发改委发布文件在全国实行“阶梯电价”收费,重庆结合本市实际,根据国家发改委文件要求,决定从2016年1月1日起对居民生活用电实行“阶梯电价”收费,具体收费标准见下表.若2016年8月份,该市居民甲生活用电240千瓦时(能量量度单位,1千瓦时即1度),交电费130元.
一户居民一个月用电量
电费价格(元/千瓦时)
第一档
不超过200千瓦时
0.52
第二档
超过200千瓦时但不超过320千瓦时

第三档
超过320千瓦时
0.95
(1)求上表中的
 的值;
的值;(2)若该市居民乙某月交电费220元,居民乙当月的生活用电量为多少千瓦时?
(3)实行“阶梯电价”收费后,该市居民丙月用电量为多少千瓦时,其当月的平均电价为0.55元/千瓦时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C在数轴上表示数a,b,c,满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是关于字母x,y的五次多项式.
(1)a的值________,b的值________,c的值________.
(2)已知蚂蚁从A点出发,途径B,C两点,以每秒3cm的速度爬行,需要多长时间到达终点C?
(3)求值:a2b﹣bc.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
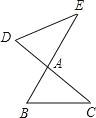
A. ∠B=∠D B. ∠C=∠E C.
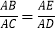 D.
D. 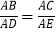
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于整式
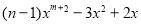 (其中m是大于
(其中m是大于 的整数).
的整数).(1)若
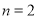 ,且该整式是关于x的三次三项式,求m的值;
,且该整式是关于x的三次三项式,求m的值;(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
-
科目: 来源: 题型:
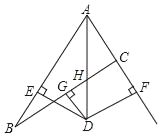
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)求证:AE=AF;
(2)求证:BE=CF;
(3)如果AB=12,AC=8,求AE的长.
相关试题

