【题目】如图,在四边形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=6,AD=9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G.设DE=x,△GEF与四边形ABCD重叠部分的面积为y.
(1)求CD的长及∠1的度数;
(2)若点G恰好在BC上,求此时x的值;
(3)求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
参考答案:
【答案】
(1)
解:如图1,

过点A作AH⊥BC于点H,
∵在Rt△AHB中,AB=6,∠B=60°,
∴AH=ABsinB=6× ![]() =3
=3 ![]() ,
,
∵∠D=∠BCD=90°,
∴四边形AHCD为矩形,
∴CD=AH=3 ![]() ,
,
∵ ![]() ,
,
∴∠CAD=30°,
∵EF∥AC,
∴∠1=∠CAD=30°
(2)
解:若点G恰好在BC上,如图2,

由对折的对称性可知Rt△FGE≌Rt△FDE,
∴GE=DE=x,∠FEG=∠FED=60°,
∴∠GEC=60°,
∵△CEG是直角三角形,
∴∠EGC=30°,
∴在Rt△CEG中,EC= ![]() EG=
EG= ![]() x,
x,
由DE+EC=CD 得 ![]() ,
,
∴x=2 ![]()
(3)
解:分两种情形:
第一种情形:当 ![]() 时,如图3,
时,如图3,

在Rt△DEF中,tan∠1=tan30°= ![]() ,
,
∴DF=x÷ ![]() =
= ![]() x,
x,
∴y=S△EGF=S△EDF= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() >0,对称轴为y轴,
>0,对称轴为y轴,
∴当 ![]() ,y随x的增大而增大,
,y随x的增大而增大,
∴当x=2 ![]() 时,y最大值=
时,y最大值= ![]() ×
× ![]() =6
=6 ![]() ;
;
第二种情形:当2 ![]() <x≤3
<x≤3
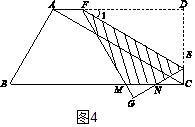
设FG,EG分别交BC于点M、N,
(法一)∵DE=x,
∴EC= ![]() ,NE=2
,NE=2 ![]() ,
,
∴NG=GE﹣NE= ![]() =
= ![]() ,
,
又∵∠MNG=∠ENC=30°,∠G=90°,
∴MG=NGtan30°= ![]() ,
,
∴ ![]() =
= ![]()
∴y=S△EGF﹣S△MNG= ![]() =
= ![]()
∵ ![]() ,对称轴为直线
,对称轴为直线 ![]() ,
,
∴当2 ![]() <x≤3
<x≤3 ![]() 时,y有最大值,且y随x的增大而增大,
时,y有最大值,且y随x的增大而增大,
∴当 ![]() 时,
时, ![]() =9
=9 ![]() ,
,
综合两种情形:由于6 ![]() <9
<9 ![]() ;
;
∴当 ![]() 时,y的值最大,y的最大值为9
时,y的值最大,y的最大值为9 ![]() .
.
【解析】(1)如图1,作辅助线AH⊥BC,AH的长就是CD的长,根据直角三角形中的特殊三角函数值可以求AH的长,即CD=AH=3 ![]() ,在直角△ACD中,求∠CAD=30°,由平行线的同位角相等可以得∠1=∠CAD=30°;(2)如图2,由对折得:Rt△FGE≌Rt△FDE,则GE=DE=x,∠FEG=∠FED=60°,从而求得直角△GEC中,EC=
,在直角△ACD中,求∠CAD=30°,由平行线的同位角相等可以得∠1=∠CAD=30°;(2)如图2,由对折得:Rt△FGE≌Rt△FDE,则GE=DE=x,∠FEG=∠FED=60°,从而求得直角△GEC中,EC= ![]() x,根据DE+EC=CD 列式可求得x的值(3)分两种情形:
x,根据DE+EC=CD 列式可求得x的值(3)分两种情形:
第一种情形:当 ![]() 时,如图3,△GEF完全在四边形内部分,重叠部分面积就是△GEF的面积;
时,如图3,△GEF完全在四边形内部分,重叠部分面积就是△GEF的面积;
第二种情形:当2 ![]() <x≤3
<x≤3 ![]() 时,如图4,重叠部分是△GEF的面积﹣△MNG的面积,所以要根据特殊的三角函数值求MG、NG的长,代入面积公式即可.
时,如图4,重叠部分是△GEF的面积﹣△MNG的面积,所以要根据特殊的三角函数值求MG、NG的长,代入面积公式即可.
再根据两种情形的最大值作对比得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于点F,连接AD、CF.
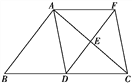
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨)
运往乙地(单位:吨)
A
x
B
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣
 x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】两位同学将一个二次三项式因式分解,一位同学因看错了一次项系数而分解成2
 ,另一位同学因看错了常数项而分解成2
,另一位同学因看错了常数项而分解成2 ,请将原多项式因式分解.
,请将原多项式因式分解. -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴
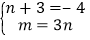
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校测量了九年级(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图如图,则下列说法不正确的是( )

A. 该班人数最多的身高段的学生数为20人
B. 该班身高低于160.5 cm的学生数为20人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
相关试题

