【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为x=1,与y轴的交点B在(0,2)和(0,3)之间(包含这两个点)运动.有如下四个结论:①抛物线与x轴的另一个交点是(3,0);②点C(x1,y1),D(x2,y2)在抛物线上,且满足x1<x2<1,则y1>y2;③常数项c的取值范围是2≤c≤3;④系数a的取值范围是﹣1≤a≤﹣![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①④ D. ①③④
参考答案:
【答案】D
【解析】
由对称轴及与x轴的一个交点,可以求出另一个交点为(3,0),又由于二次函数与y轴的交点为(c,0),且交点在(0,2)和(0,3)之间,从而得到c的范围,再结合两根之积![]() 可以求出a的范围.
可以求出a的范围.
∵抛物线与y轴的交点在(0,2)和(0,3)之间,∴2≤c≤3,∴③正确,排除C选项.∵对称轴为x=1,且其与x轴的一个交点为(-1,0),∴另一个交点为2![]() -(-1)=3,∴抛物线与x轴的另一个交点为(3,0),∴①正确,排除B选项.由根与系数的关系可知两根之积为
-(-1)=3,∴抛物线与x轴的另一个交点为(3,0),∴①正确,排除B选项.由根与系数的关系可知两根之积为![]() ,且2≤c≤3,∴2≤-3a≤3,∴﹣1≤a≤﹣
,且2≤c≤3,∴2≤-3a≤3,∴﹣1≤a≤﹣![]() ,∴④正确,排除A,故选D.
,∴④正确,排除A,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点列达终点时,另一点也停止运动,设运动的时间为t秒.
(1)求线段DO的长;
(2)设运动过程中△POQ两直角边的和为y,请求出y关于x的函数解析式;
(3)请直接写出点P在线段OC上,点Q在线段DO上运动时,△POQ面积的最大值,并写出此时的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx+m2+1(m为常数),当自变量x的值满足﹣3≤x≤﹣1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或﹣3 B. ﹣3或﹣5 C. 1或﹣1 D. 1或﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )
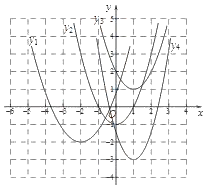
A. y1 B. y2 C. y3 D. y4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若
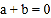 .
.①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.

-
科目: 来源: 题型:
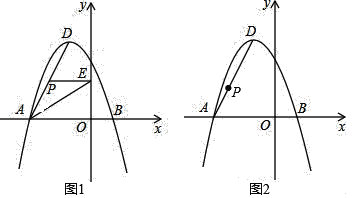
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:
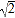 =1.41,
=1.41,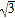 =1.73,
=1.73,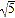 =2.24)
=2.24)(2)求此矩形养鸡场的最大面积.

相关试题

