搜索
【题目】在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（ ）
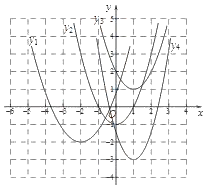
A. y1 B. y2 C. y3 D. y4
参考答案：
【答案】A
【解析】
由图象的点的坐标，根据待定系数法求得解析式即可判定．
由图象可知：
抛物线y1的顶点为（-2，-2），与y轴的交点为（0，1），根据待定系数法求得y1=
（x+2）2-2；
抛物线y2的顶点为（0，-1），与x轴的一个交点为（1，0），根据待定系数法求得y2=x2-1；
抛物线y3的顶点为（1，1），与y轴的交点为（0，2），根据待定系数法求得y3=（x-1）2+1；
抛物线y4的顶点为（1，-3），与y轴的交点为（0，-1），根据待定系数法求得y4=2（x-1）2-3；
综上，解析式中的二次项系数一定小于1的是y1
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线G：y=ax2-4ax+3a-2（a≠0），其顶点为C，直线l：y=ax-2a+1（a≠0）与x轴、y轴分别交于A，B两点．
（1）当抛物线G的顶点C在x轴上时，求a的值；
（2）当a＞0时，若△ABC的面积为2，求a的值；
（3）若点Q（m，n）在抛物线G上，把抛物线G绕着点P（t，-2）旋转180°，在1≤m≤3时，总有n随着m的增大而增大，请直接写出t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在△ABC中，AB=AC，∠BAC=α，直线l经过点A（不经过点B或点C），点C关于直线l的对称点为点D，连接BD，CD．
（1）如图1，
①求证：点
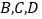在以点
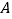为圆心，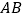
为半径的圆上.②直接写出∠BDC的度数（用含α的式子表示）为___________.
（2）如图2，当α=60°时，过点D作BD的垂线与直线l交于点E，求证：AE=BD；
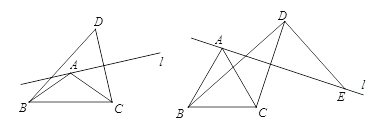
图1 图2
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，点A在直线l上，以A为圆心，OA为半径的圆与y轴的另一个交点为E．给出如下定义：若线段OE，⊙A和直线l上分别存在点B，点C和点D，使得四边形ABCD是矩形（点A，B，C，D顺时针排列），则称矩形ABCD为直线l的“位置矩形”．
例如，图中的矩形ABCD为直线l的“位置矩形”．
（1）若点A（-1，2），四边形ABCD为直线x=-1的“位置矩形”，则点D的坐标为 ；
（2）若点A（1，2），求直线y=kx+1（k≠0）的“位置矩形”的面积；
（3）若点A（1，-3），直线l的“位置矩形”面积的最大值为 ，此时点D的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一定时间后，测试出这种植物高度的增长情况，部分数据如下表：
温度t/℃
…
﹣5
﹣3
2
…
植物高度增长量h/mm
…
34
46
41
…
科学家推测出h（mm）与t之间的关系可以近似地用二次函数来刻画．已知温度越适合，植物高度增长量越大，由此可以推测最适合这种植物生长的温度为（ ）
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司试销一种成本单价为50元/件的新产品，规定试销时销售单价不低于成本单价，又不高于80元/件，经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y＝kx+b的关系（如图所示）
（I）根据图象，求一次函数y＝kx+b的解析式，并写出自变量x的取值范围；
（Ⅱ）该公司要想每天获得最大的利润，应把销售单价定为多少？最大利润值为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t2．
（1）求小球飞行3s时的高度；
（2）问：小球的飞行高度能否达到22m？请说明理由．
相关试题
