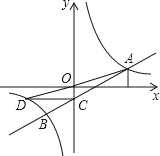
【题目】如图,一次函数y=ax+b与反比例函数y=![]() 的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为
的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为![]() ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
参考答案:
【答案】(1)y=![]() x-1;反比例函数的解析式为 y=
x-1;反比例函数的解析式为 y=![]() ,(2)18.
,(2)18.
【解析】
试题(1)根据∠AOE的正切值求出点A的坐标,根据点A坐标求出反比例函数解析式,从而得出点B的坐标,然后根据点A、点B的坐标得出一次函数解析式;(2)首先求出点C和点D的坐标,然后将四边形的面积转化成△ODC和△BDC的面积和进行求解.
试题解析:(1)tan∠AOE=![]() ,OE=6,A(6,2),y=
,OE=6,A(6,2),y=![]() 的图象过A(6,2),∴
的图象过A(6,2),∴![]() ,k=12,
,k=12,
∴反比例函数的解析式为 y=![]() , ∵B(﹣4,n)在 y=
, ∵B(﹣4,n)在 y=![]() 的图象上, ∴ n=﹣3,B(﹣4,﹣3),
的图象上, ∴ n=﹣3,B(﹣4,﹣3),
一次函数y=ax+b过A、B点,则![]() 解得:
解得: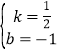
∴一次函数解析式为y=![]() x-1;
x-1;
当x=0时,y=﹣1,C(0,﹣1), 当y=﹣1时,x=﹣12,D(﹣12,﹣1),
![]() =
=![]() +
+![]() =12×1÷2+12×2÷2=6+12=18
=12×1÷2+12×2÷2=6+12=18
-
科目: 来源: 题型:
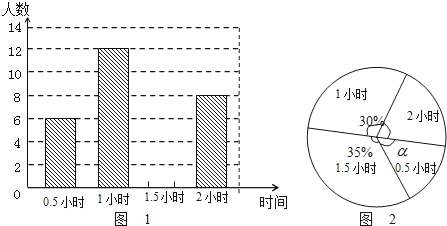
查看答案和解析>>【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.
(1)求证:FE⊥AB;
(2)当AE=6,sin∠CFD=
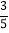 时,求EB的长.
时,求EB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在
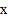 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 抛物线
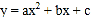 与
与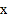 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与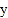 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①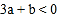 ;②
;②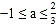 ;③对于任意实数m,
;③对于任意实数m,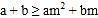 总成立;④关于
总成立;④关于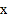 的方程
的方程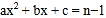 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为

A. 1 个 B. 2 个 C. 3 个 D. 4 个
相关试题

