【题目】如图1,![]() 和
和![]() 都是等边三角形
都是等边三角形

(1)求证:四边形![]() 是菱形
是菱形
(2)给![]() 方向将
方向将![]() 平移到
平移到![]() 的位置如图2,此时,四边形
的位置如图2,此时,四边形![]() (如图3)是平行四边形吗?
(如图3)是平行四边形吗?
(3)若按(2)题的方式继续平移![]() 到
到![]() ,当在什么位置时,四边形
,当在什么位置时,四边形![]() 是矩形,请画出
是矩形,请画出![]() 的位置(如图4),并证明你的结论
的位置(如图4),并证明你的结论
参考答案:
【答案】(1)见解析;(2)是平行四边形;(3)四边形ABD2C2是矩形,证明和图见解析
【解析】
(1)根据△ABC和△DBC都是等边三角形,得AB=BC=CD=DA,从而证明是菱形;
(2)根据平移知△B1C1D1≌△BCD,再证AB//C1D1,从而证明是平行四边形;
(3)先证B、C、C2三点共线和A、C、D2三点共线,从而证明AD2=BC2且相互平分即可证明是矩形.
证明:(1)∵△ABC和△DBC都是等边三角形,
∴AB=BC=CA,BD=BC=CD,
∴AB=BC=CD=DA,
∴四边形ABDC是菱形;
(2)是平行四边形,证明如下:
∵△B1C1D1是△BCD沿BC方向平移的,
∴△B1C1D1≌△BCD,
∵∠ABC1=∠B1C1D1=60![]() ,
,
∴AB//C1D1,
∵AB=C1D1,
∴四边形AB D1C1是平行四边形;
(3)如图,当C点与B2重合时,四边形ABD2C2是矩形,证明如下:
∵△B2D2C2是沿着BC方向平移,
∴B、C、C2三点共线,
∴∠BCC2=180![]() ,
,
∴∠DCD2=180![]() -∠BCD-∠C2CD2=60
-∠BCD-∠C2CD2=60![]() ,
,
∴∠ACD2=∠ACB+∠BCD+∠DCD2=180![]() ,
,
∴A、C、D2三点共线,
∴AD2=AC+CD2,BC2=BC+CC2,
∵AC=CD2=BC=CC2,
∴AD2=BC2且相互平分,
∴四边形ABD2C2是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点的坐标分别是A(0,1),B(2,0),C(2,3).将三角形ABC先向左平移3个单位 ,再向下平移5个单位得三角形
 .
.(1)画出
 ;
;(2)求△ABC的面积;
(3)若点P在y轴上,且△ABP的面积等于△ABC的面积,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论: ①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.
其中正确的是( )
A.①④
B.②④
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发.他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示.根据图象信息,以下说法错误的是( )

A.他们都骑了20 km
B.两人在各自出发后半小时内的速度相同
C.甲和乙两人同时到达目的地
D.相遇后,甲的速度大于乙的速度
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求
 的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:
的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设: ……①
……①然后在①式的两边都乘以6,得:
 ……②
……②②-①得
 ,即
,即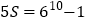 ,所以
,所以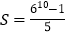 .
.得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出
 的值?你的答案是
的值?你的答案是A.
 B.
B.  C.
C.  D.
D. 
相关试题

