Question

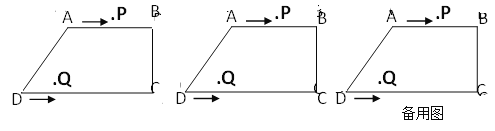
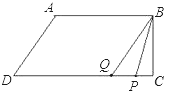
【题目】在直角梯形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm。点P从点A出发，以每秒3cm的速度沿折线ABCD运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动。已知动点P，Q同时出发，当点Q运动到点C时，P，Q运动停止，设运动时间为t秒.

（1）求CD的长.

（2）t为何值时？四边形PBQD为平行四边形.

（3）在点P，点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由.

Answer 1

【答案】（1）16；（2）；（3）.

【解析】试题分析：（1）过点A作AM⊥CD于M，四边形AMCB是矩形，AM=BC,AD是已知的，根据勾股定理求出DM,CM=AB,所以CD就求出来了；（2）当四边形PBQD为平行四边形时,点P在AB上，点Q在DC上，用t表示出BP,DQ的长，满足BP=DQ,求出t值，则BP,DQ即可求出，然后求出CQ,用勾股定理求出BQ，四边形PBQD的周长就求出来了；（3）D从Q到C需要8秒，所以t的范围是0≤t≤8,Q根据P所在线段不同，分三种情况讨论，即①当点P在线段AB上时，即时，用t表示出BP的长，列三角形BPQ的面积等于20的方程求解；②当点P在线段BC上时，即时，用t表示出BP,CQ的长，建立三角形BPQ的面积等于20的方程求解；③当点P在线段CD上时，因为他们相遇的时间是，若点P在Q的右侧，即6≤t≤，用t表示出PQ的长，进而列出面积方程式求解；若点P在Q的左侧，即，用t表示出PQ的长，列出面积方程式求解．

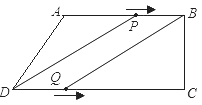
试题解析：（1）过点A作AM⊥CD于M，根据勾股定理，AD=10，AM=BC=8，∴DM==6，∴CD=16；（2）当四边形PBQD为平行四边形时，点P在AB上，点Q在DC上，如图，由题知：AP=3t,BP=10﹣3t，DQ=2t，∴10﹣3t=2t，解得t=2，此时，BP=DQ=4，CQ=12，∴，∴四边形PBQD的周长=2（BP+BQ）=；

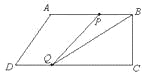
（3）①当点P在线段AB上时，到B点时是秒，即时，如图，BP=10﹣3t，BC=8，∴，∴．

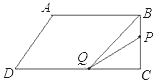
②当点P在线段BC上时，P到达C点t值时6秒，即时，如图，BP=AB+BP-AB=3t﹣10，DQ=2t,CQ=16﹣2t，∴，化简得：3t2﹣34t+100=0，△=﹣44＜0，所以方程无实数解．此种情况不存在三角形BPQ的面积是20；

③当点P在线段CD上时，P点与Q点相遇时,可列2t+3t=10+8+16,t=,相遇时间是，若点P在Q的右侧，即6≤t≤，则有PQ=34-（2t+3t）=34﹣5t，于是，解此方程得：

＜6，舍去，若点P在Q的左侧，即，则有PQ=2t+3t-34=5t﹣34，可列方程：，解得：t=7．8．∴综合得出满足条件的t值存在，其值分别为，t2=7．8．