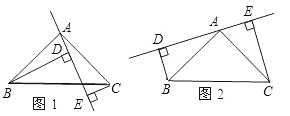
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.
(1)如图1,△ABD与与△CAE全等吗?请说明理由;
(2)如图1,BD=DE+CE成立吗?为什么?
(3)若直线AE绕A点旋转到如图2位置时,其它条件不变,BD与DE、CE关系如何?请说明理由.
参考答案:
【答案】(1)△ABD≌△CAE;(2)成立;(3)DE=BD+CE.
【解析】
(1)根据已知条件易证得∠BAD=∠ACE,且根据全等三角形的判定可证明△ABD≌△CAE;
(2)根据全等三角形的性质及各线段的关系即可得结论.
(3)DE=BD+CE.根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(1)△ABD≌△CAE,理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵CE⊥AE,∴∠ACE+∠CAE=90°,∴∠ACE=∠BAD;
又∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
在△ABD和△CAE中,∵∠BAD=∠ACE,∠ADB=∠CEA,AB=CA,∴△ABD≌△CAE(AAS);
(2)成立,理由如下:
∵△ABD≌△CAE,∴BD=AE,AD=CE;
∵AE=DE+AD,∴BD=DE+CE;
(3)DE=BD+CE.理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵CE⊥AE,∴∠ACE+∠CAE=90°,∴∠ACE=∠BAD;
又∵BD⊥AE,CE⊥AE,∴∠ADB=∠CEA=90°.
在△ABD和△CAE中,∵∠BAD=∠ACE,∠ADB=∠CEA,AB=CA,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE;
∵DE=AE+AD,∴DE=BD+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.已知:在矩形
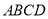 中,
中,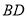 是对角线,
是对角线,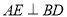 于点
于点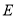 ,
,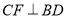 于点
于点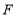 ;
;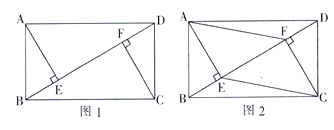
(1)如图1,求证:
 ;
;(2)如图2,当
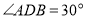 时,连接
时,连接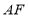 .
.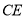 ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形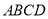 面积的
面积的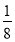 .
. -
科目: 来源: 题型:
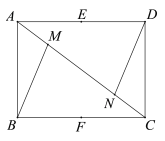
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4.M、N在对角线AC上,且AM=CN,E、F分别是AD、BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
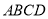 的边
的边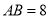 ,
, 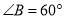 ,
, 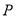 是
是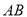 上一点,
上一点, 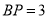 ,
, 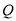 是
是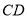 边上一动点,将梯形
边上一动点,将梯形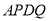 沿直线
沿直线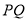 折叠,
折叠, 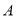 的对应点为
的对应点为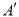 ,当
,当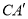 的长度最小时,
的长度最小时, 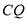 的长为__________.
的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.则AD与BE的数量关系为 ;∠AEB的度数为 度.
(2)拓展探究:如图2,如果△ACB和△CDE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,判断线段AE与BE的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
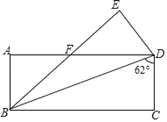
A. 62°B. 56°C. 31°D. 28°
相关试题

