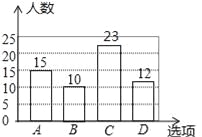
【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
参考答案:
【答案】(1)60;(2)作图见解析;(3)1380.
【解析】试题分析:(1)由A的人数及其人数占被调查人数的百分比可得;
(2)根据各项目人数之和等于总数可得C选项的人数;
(3)用样本中最想去湿地公园的学生人数占被调查人数的比例乘总人数即可.
试题解析:(1)本次调查的样本容量是15÷25%=60;
(2)选择C的人数为:60﹣15﹣10﹣12=23(人),
补全条形图如图:
(3)![]() ×3600=1380(人).
×3600=1380(人).
答:估计该校最想去湿地公园的学生人数约由1380人.
-
科目: 来源: 题型:
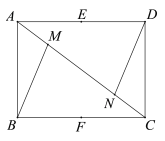
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4.M、N在对角线AC上,且AM=CN,E、F分别是AD、BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 的边
的边 ,
, 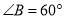 ,
,  是
是 上一点,
上一点, 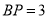 ,
, 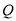 是
是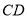 边上一动点,将梯形
边上一动点,将梯形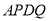 沿直线
沿直线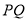 折叠,
折叠, 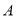 的对应点为
的对应点为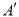 ,当
,当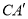 的长度最小时,
的长度最小时, 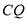 的长为__________.
的长为__________.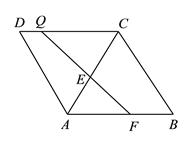
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.
(1)如图1,△ABD与与△CAE全等吗?请说明理由;
(2)如图1,BD=DE+CE成立吗?为什么?
(3)若直线AE绕A点旋转到如图2位置时,其它条件不变,BD与DE、CE关系如何?请说明理由.
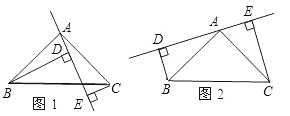
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.则AD与BE的数量关系为 ;∠AEB的度数为 度.
(2)拓展探究:如图2,如果△ACB和△CDE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,判断线段AE与BE的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
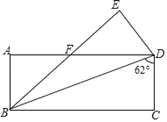
A. 62°B. 56°C. 31°D. 28°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

相关试题

