【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
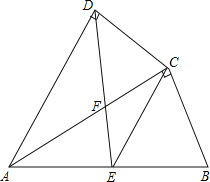
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
参考答案:
【答案】解:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB。
∵∠ADC=∠ACB=90°,∴△ADC∽△ACB。
∴![]() ,即AC2=ABAD。
,即AC2=ABAD。
(2)证明:∵E为AB的中点,∴CE=![]() AB=AE。∴∠EAC=∠ECA。
AB=AE。∴∠EAC=∠ECA。
∵∠DAC=∠CAB,∴∠DAC=∠ECA。∴CE∥AD。
(3)∵CE∥AD,∴△AFD∽△CFE,∴![]() 。
。
∵CE=![]() AB,∴CE=
AB,∴CE=![]() ×6=3。
×6=3。
∵AD=4,∴![]() 。∴
。∴![]() 。
。
【解析】(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD。
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
AB=AE,从而可证得∠DAC=∠ECA,得到CE∥AD。
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值,从而得到
的值,从而得到![]() 的值。
的值。
-
科目: 来源: 题型:
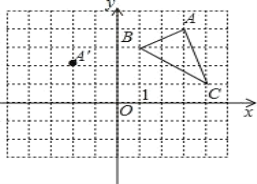
查看答案和解析>>【题目】在平面直角坐标系中,△ABC 的三个顶点的位置如图所示,点 A′的坐标是(-2,2),现将△ABC 平移,使点 A 变换为点 A′,点 B′、C′分别是 B、C 的对应点.
(1) 请画出平移后的△A′B′C′(不写画法),并直接写出点B′、C′的坐标:B′ 、C′ ;
(2) 若△ABC 内部一点 P 的坐标为(
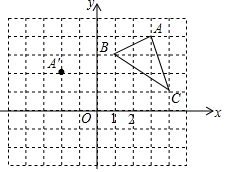 ,
,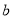 ),则点 P 的对应点 P′的坐标是 ;
),则点 P 的对应点 P′的坐标是 ;(3) 连接 A′B,CC′,并求四边形 A′BCC′的面积.
-
科目: 来源: 题型:
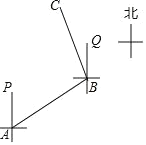
查看答案和解析>>【题目】为全力推进农村公路快速发展,解决农村“出行难”问题,现将 A、B、C 三村连通的公路进行硬化改造(如图所示),铺设成水泥路面.已知 B 村在 A 村的北偏东 60°方向上,∠ABC=110°.
(1)C 村在 B 村的什么方向上?
(2)甲、乙两个施工队分别从 A 村、C 村向 B 村施工,两队的施工进度相同A 村到 B 村的距离比 C 到 B 村的距离多 400 米,甲队用了 9 天完成铺设任务乙队用了 7 天完成铺设任务,求两段公路的总长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠1=∠2,EG 平分∠AEC.
(1)如图1,∠MAE=50°,∠FEG=15°,∠NCE=80°.试判断 EF 与 CD 的位置关系,并说明理由.
(2)如图2,∠MAE=135°,∠FEG=30°,当 AB∥CD 时,求∠NCE 的度数;
(3)如图2,试写出∠MAE、∠FEG、∠NCE 之间满足什么关系时,AB∥CD.
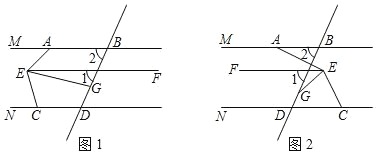
-
科目: 来源: 题型:
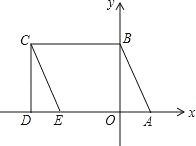
查看答案和解析>>【题目】如图所示,A(2,0),点 B 在 y 轴上,将三角形 OAB 沿 x 轴负方向平移,平移后的图形为三角形 DEC,且点 C 的坐标为(-6,4) .
(1)直接写出点 E 的坐标 ;
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿“BC→CD”移动.若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒,回答下列问题:
①求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);
②当 3 秒<t<5 秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z 之间的数量关系能否确定?若能,请用含 x,y 的式子表示 z,写出过程;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
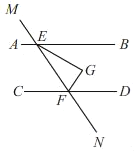
A. 20°B. 25°C. 35°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
相关试题

