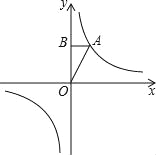
【题目】如图,已知反比例函数y=![]() (k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(1)求m,k的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=![]() 的图象有两个不同的公共点,求实数n的取值范围.
的图象有两个不同的公共点,求实数n的取值范围.
参考答案:
【答案】(1)、m=2;k=2;(2)、:n>﹣![]() 且n≠0
且n≠0
【解析】
试题分析:(1)、根据三角形的面积公式即可求得m的值;(2)、若一次函数y=nx+2(n≠0)的图象与反比例函数y=![]() 的图象有两个不同的公共点,则方程
的图象有两个不同的公共点,则方程![]() =nx+2有两个不同的解,利用根的判别式即可求解.
=nx+2有两个不同的解,利用根的判别式即可求解.
试题解析:(1)、由已知得:S△AOB=![]() ×1×m=1, 解得:m=2,
×1×m=1, 解得:m=2,
把A(1,2)代入反比例函数解析式得:k=2;
(2)、由(1)知反比例函数解析式是y=![]() ,
,
由题意得: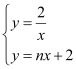 有两个不同的解,即
有两个不同的解,即![]() =nx+2有两个不同的解, 方程去分母,得:nx2+2x﹣2=0,
=nx+2有两个不同的解, 方程去分母,得:nx2+2x﹣2=0,
则△=4+8n>0, 解得:n>﹣![]() 且n≠0.
且n≠0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A.k≤﹣4
B.k≥﹣4
C.k≤4
D.k>4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法: ①a>0;②c>0;③4a﹣b+c<0;④当﹣1<x<3时,y>0.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
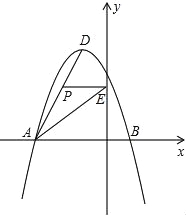
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
-
科目: 来源: 题型:
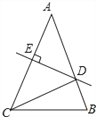
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A=40°,求∠DCB的度数;
(2)若AE=5,△DCB的周长为16,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个直角三角形中,有一个锐角等于40°,则另一个锐角的度数是( )
A. 40°B. 50°C. 60°D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2-4=__________.
相关试题

