Question

【题目】如图1，在等腰Rt△ABC中，∠ACB=90°，点F是AB上一点，作等腰Rt△FCP，且∠PCF=90°，连结AP．

（1）求证：△CFB≌△CPA；

（2）求证：AP2+AF2=PF2；

（3）如图2，在AF上取点E，使∠ECF=45°，求证：AE2+BF2=EF2．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.

【解析】

（1）由△ABC和△PCF都是等腰直角三角形，易得AC=BC，PC=FC，∠ACP=∠BCF可得结论；

(2) 由（1）可得∠PAC=∠B=45°，可得∠PAF=∠PAC+∠BAC=45°+45°=90°，AP2+AF2=PF2；

（3）连结PE，可证得△PCE≌△FCE（SAS），可得EF=EP，∠PCE=∠ECF=45°，由（2）知可得∠PAF=90°，PA=BF，AP2+AE2=PE2，AE2+BF2=EF2.

解：

（1）证明：∵△ABC和△PCF都是等腰直角三角形，

∴AC=BC，PC=FC，∠ACB=PCF=90°，

∴∠ACB-∠ACF=∠PCF-∠ACF，

∴∠ACP=∠BCF，

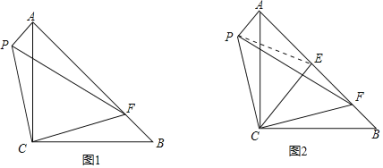
在△CFB与△CPA中

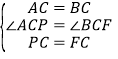
∴△CFB≌△CPA（SAS）

（2）证明：∵△ABC是等腰直角三角形，

∴∠B=∠BAC=45°，

由（1）△CFB≌△CPA，∴∠PAC=∠B=45°，

∴∠PAF=∠PAC+∠BAC=45°+45°=90°，

∴AP2+AF2=PF2

（3）证明：连结PE，

∵∠ACE+∠BCF=∠ACB-∠ECF=90°-45°=45°，

∵∠BCF=∠ACP，

∴∠PCE=∠PCA+∠ACE=45°，

在△PCE与△FCE中

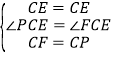
∴△PCE≌△FCE（SAS），

∴EF=EP，∠PCE=∠ECF=45°

由（2）知∴∠PAF=90°，PA=BF，

∴AP2+AE2=PE2；

∴AE2+BF2=EF2 ．