【题目】根据要求回答问题：
（1）已知：等边△ABC的边长为4，点P在线段AB上，点D在线段AC上，且△PDE为等边三角形，当点P与点B重合时（如图1），AD+AE的值为；
（2）[类比探究]在上面的问题中，如果把点P沿BA方向移动，使PB=1，其余条件不变（如图2），AD+AE的值是多少？请写出你的计算过程；
（3）[拓展迁移]如图3，△ABC中，AB=BC，∠ABC=a，点P在线段BA延长线上，点D在线段CA延长线上，在△PDE中，PD=PE，∠DPE=a，设AP=m，则线段AD、AE有怎样的等量关系？请用含m，a的式子直接写出你的结论．

参考答案：

【答案】
（1）4
（2）解：AD+AE=3

理由：如图2中，作PK∥BC交AC于K．连接AE．

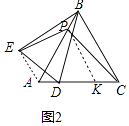
易证△PAK是等边三角形，

由上面题目可知．AE+AD=AK=3


（3）解：如图3中，作PJ⊥AD于J，在AD上取一点K，使得PK=PA．

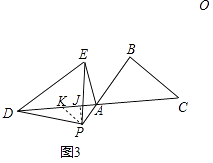
易证∠APK=∠DPE=α，

∵PD=PE，PK=PA，

∴∠DPK=∠EPA，

∴△PDK≌△PEA，

∴DK=AE，

∴AD﹣AE=AK=2AJ=2msin ．

∴AD﹣AE=2msin


【解析】（1）解：如图1中，

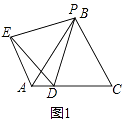
∵△PDE．△PAC都是等边三角形，

∴PE=PD，PA=PC，∠EPD=∠APC=60°，

∴∠EPA=∠DPC，

∴△EPA≌△DPC，

∴AE=CD，

∴AD+AE=AD+DC=AC=4．

【考点精析】本题主要考查了等边三角形的性质的相关知识点，需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．

关闭