[题目]如图.∠AOB＝56°.OC平分∠AOB.如果射线OA上的点E满足△OCE是等腰三角形.那么∠OEC的度数为．题目和参考答案 ——青夏教育精英家教网—

【题目】如图，∠AOB＝56°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为________________．

参考答案：

【答案】124°或76°或28°

【解析】

题目要求∠OEC的度数，而没有告诉∠OEC是等腰△OCE的顶角还是底角，由此此题要分类讨论;由角平分线的定义先求出∠AOC的度数，再分OE=CE、OC=CE、OE=OC进行讨论，结合等腰三角形的性质和三角形的内角和定理即可求出∠OEC的度数.

∵∠AOB=56°，0C平分∠AOB,

∴∠AOC=28°,

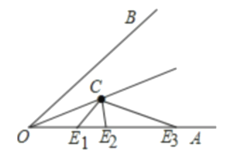
①当E在时，OE=CE,

∵∠AOC=∠OCE=28°

∴∠OEC'=180°-28°-28°=124°，

②当E在点时，OC=OE,可得：

③当E在时，OC'=CE,

则∠OEC=∠A0C=28°,

故答案为: 124°或76°或28°.

【点睛]

本题考查等腰三角形内角的题目，解决本题的关键是结合等腰三角形的性质和三角形内角和定理解答.

相关试题

科目： 来源： 题型：

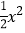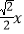【题目】如图，抛物线y=﹣++2与x轴相交于A，B两点，（点A在B点左侧）与y轴交于点C．
（1）求A，B两点坐标．
（2）连结AC，若点P在第一象限的抛物线上，P的横坐标为t，四边形ABPC的面积为S．试用含t的式子表示S，并求t为何值时，S最大．
（3）在（2）的基础上，在整条抛物线上和对称轴上是否分别存在点G和点H，使以A，G，H，P四点构成的四边形为平行四边形？若存在，请直接写出G，H的坐标；若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，点C是线段AB上一点，分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE，连结AE和BD，相交于点F.
（1）求证：AE=BD；
（2）如图2.固定△BCE不动，将等边△ACD绕点C旋转（△ACD和△BCE不重叠），试问∠AFB的大小是否变化?请说明理由；
（3）在△ACD旋转的过程中，以下结论：①CG=CH；② GF=HF； ③FC平分分∠GCH；④FC平分∠GFH；一定正确的有（填写序号，不要求证明）
查看答案和解析>>
科目： 来源： 题型：

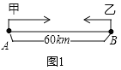
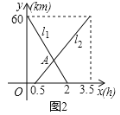
【题目】A、B两地相距60km,甲从A地去B地，乙从B地去A地，图中l1、l2分别表示甲、乙两人离B地的距离y（km）与甲出发时间x（h）的函数关系图象.
（1）根据图象，直接写出乙的行驶速度；
（2）解释交点A的实际意义；
（3）甲出发多少时间，两人之间的距离恰好相距5km；
（4）若用y3（km）表示甲乙两人之间的距离，请在坐标系中画出y3（km）关于时间x（h）的函数关系图象，注明关键点的数据.

查看答案和解析>>
科目： 来源： 题型：

【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
（1）求每辆大客车和每辆小客车的乘客座位数；
（2）由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目： 来源： 题型：

【题目】平面直角坐标系xOy中，过原点O及点A（0，4）、C（12，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒2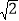个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒4个单位长度的速度沿x轴正方向移动．设移动时间为t秒．
（1）当点P移动到点D时，求出此时t的值．
（2）当t为何值时，△PQB为直角三角形．
（3）已知过O、P、Q三点的抛物线解析式为y=﹣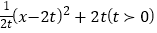．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE.
（1）求证：△DEF是等腰三角形；
（2）当∠A=36°时，求∠DEF的度数.
查看答案和解析>>