【题目】如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.
(1)若点D是AC的中点,如图1,求证:AD=CE
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F)

参考答案:
【答案】(1)证明见解析;(2)AD=CE,证明见解析.
【解析】分析:(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;(2)过D作DF∥BC,交AB于F,证△BFD≌△DCE,推出DF=CE,证△ADF是等边三角形,推出AD=DF,即可得出答案.
本题解析:
(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∵D为AC中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE,
∴∠CDE=30°=∠E,∴CD=CE,∵AD=DC,∴AD=CE;
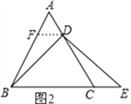
(2)AD=CE,如图2,过D作DF∥BC,交AB于F,
则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,
∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°﹣60°=120°,
∵DF∥BC,∴∠FDB=∠DBE=∠E,
在△BFD和△DCE中 ,∴△BFD≌△DCE,∴CE=DF=AD,即AD=CE.
,∴△BFD≌△DCE,∴CE=DF=AD,即AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知开始输入的x的值为正整数.若最后输出的结果为144,则满足条件的x的值为________;若经过一次运算就能输出结果,则x的最小值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座大客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座大客车日租金为每辆300元.
求:(1)初一年级学生有多少人? 原计划租用45座客车多少辆?
(2)要使每个学生都有座位,怎样租用更合算?最低租金是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简下列多项式:
(1)
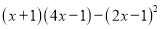
(2)
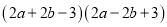
(3)若
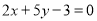 ,求
,求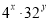 的值.
的值.(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式:
(1)4(2x-1)<3(4x+2);
(2)4(x-1)>5x-6;
(3)
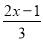 <1-
<1-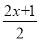 ;
;(4)10-
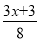 ≥9+
≥9+
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
-
科目: 来源: 题型:
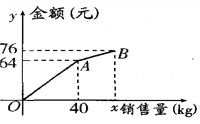
查看答案和解析>>【题目】小李以0.8元/kg的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与销售量之间的关系如图所示,那么小李赚了__________元
相关试题

