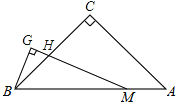
【题目】如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=![]() ∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
参考答案:
【答案】4.
【解析】
试题分析:如图,作MD⊥BC于D,延长DE交BG的延长线于E,∵△ABC中,∠C=90°,CA=CB,∴∠ABC=∠A=45°,∵∠GMB=![]() ∠A,∴∠GMB=
∠A,∴∠GMB=![]() ∠A=22.5°,∵BG⊥MG,∴∠BGM=90°,∴∠GBM=90°﹣22.5°=67.5°,∴∠GBH=∠CBM﹣∠ABC=22.5°.∵MD∥AC,∴∠BMD=∠A=45°,∴△BDM为等腰直角三角形,∴BD=DM,而∠GBH=22.5°,∴GM平分∠BMD,而BG⊥MG,∴BG=EG,即BG=
∠A=22.5°,∵BG⊥MG,∴∠BGM=90°,∴∠GBM=90°﹣22.5°=67.5°,∴∠GBH=∠CBM﹣∠ABC=22.5°.∵MD∥AC,∴∠BMD=∠A=45°,∴△BDM为等腰直角三角形,∴BD=DM,而∠GBH=22.5°,∴GM平分∠BMD,而BG⊥MG,∴BG=EG,即BG=![]() BE,∵∠MHD+∠HMD=∠E+∠HMD=90°,∴∠MHD=∠E,∵∠GBD=90°﹣∠E,∠HDM=90°﹣∠E,∴∠GBD=∠HDM,∴在△BED和△MHD中,∵∠E=∠MHD,∠EBD=∠HMD,BD=MD,∴△BED≌△MHD(AAS),∴BE=MH,∴BG=
BE,∵∠MHD+∠HMD=∠E+∠HMD=90°,∴∠MHD=∠E,∵∠GBD=90°﹣∠E,∠HDM=90°﹣∠E,∴∠GBD=∠HDM,∴在△BED和△MHD中,∵∠E=∠MHD,∠EBD=∠HMD,BD=MD,∴△BED≌△MHD(AAS),∴BE=MH,∴BG=![]() MH=4.故答案为:4.
MH=4.故答案为:4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+3b=5ab
B.a2a3=a5
C.(2a)3=6a 3
D.a6+a3=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.

(1)把﹣16,9,16,﹣5,﹣9,5分别填入图中的六个小正方形中;
(2)若某相对两个面上的数字分别为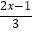 和
和 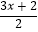 ﹣5,求x的值.
﹣5,求x的值. -
科目: 来源: 题型:
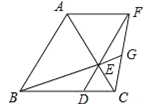
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口
运费(元/吨)
甲库
乙库
A港
14
20
B港
10
8
(1)设从甲仓库运送到A港口的物资为x吨,用含x的式子填写下表:港口
运费(元/吨)
甲库
乙库
A港
x
B港
(2)求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围;
(3)求出最低费用,并说明费用最低时的调配方案. -
科目: 来源: 题型:
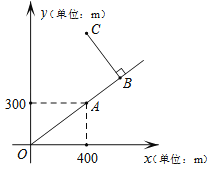
查看答案和解析>>【题目】如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是 .
相关试题

