【题目】如图,直线y1=-x-2交x轴于点A,交y轴于点B,抛物线y2=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)求当y1≥y2时x的值.

参考答案:
【答案】(1)y2=-![]() x2-2x-2(2)x≤-2或x≥0.
x2-2x-2(2)x≤-2或x≥0.
【解析】(1)由于点A是抛物线的顶点,可将抛物线的解析式设为顶点式,然后将B点坐标代入即可求出二次函数的解析式;
(2)结合A、B的坐标以及两个函数的图象,即可判断出y1≥y2时x的取值范围.
解:(1)∵直线y1=-x-2交x轴于点A,交y轴于点B,
∴点A的坐标为(-2,0),点B的坐标为(0,-2).
∵抛物线y2=ax2+bx+c的顶点为A,
∴设抛物线为y2=a(x+2)2,
∵抛物线过点B(0,-2),
∴-2=4a,a=-![]() .
.
∴y2=-![]() (x+2)2=-
(x+2)2=-![]() x2-2x-2.
x2-2x-2.
(2)当y1≥y2时,x的取值范围是x≤-2或x≥0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18
 的条件下生长最快的新品种.如图,是某天恒温系统从开启到关闭及关闭后,大棚内温度y(
的条件下生长最快的新品种.如图,是某天恒温系统从开启到关闭及关闭后,大棚内温度y( )随时间x(小时)变化的函数图象,其中BC段足双曲线
)随时间x(小时)变化的函数图象,其中BC段足双曲线 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)恒温系统这天保持大棚内温度18
 的时间有多少小时?
的时间有多少小时?(2)求k值;
(3)当x=15时,大棚内的温度约为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围。
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,一次函数y=ax+c和二次函数y=a(x+c)2的图象大致为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8 cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值_____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
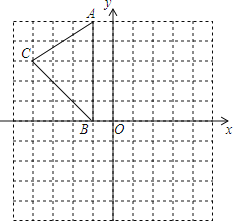
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在y轴上画出点P,使PA+PC最小;
(4)求六边形AA1C1B1BC的面积.. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
相关试题

