【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米
千米![]() 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米![]() 小时,设客车行驶时间为
小时,设客车行驶时间为![]() 小时
小时![]()
![]() 当
当![]() 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米![]() 用含a的代数式表示
用含a的代数式表示![]()
![]() 已知
已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
![]() 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间;![]() 列方程解答
列方程解答![]()
![]() 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
参考答案:
【答案】![]() 客车与乙城的距离为
客车与乙城的距离为![]() 千米;
千米;![]() 客车的行驶时间是
客车的行驶时间是![]() 小时或
小时或![]() 小时;
小时;![]() 小王选择方案二能更快到达乙城
小王选择方案二能更快到达乙城![]()
【解析】
第一问用代数式表示,第二问中用到了一元一次方程的知识,也用到了相遇的知识,要求会画图形,数形结合更好的解决相遇问题.
![]() 当
当![]() 时,客车与乙城的距离为
时,客车与乙城的距离为![]() 千米;
千米;
![]() 解:设当客车与出租车相距100千米时客车的行驶时间是t小时
解:设当客车与出租车相距100千米时客车的行驶时间是t小时
a:当客车和出租车没有相遇时
![]()
解得:![]()
b:当客车和出租车相遇后
![]()
解得:![]()
当客车与出租车相距100千米时客车的行驶时间是![]() 小时或
小时或![]() 小时
小时
![]() 小王选择方案二能更快到达乙城
小王选择方案二能更快到达乙城![]() 解:设客车和出租车x小时相遇
解:设客车和出租车x小时相遇
![]()
![]() ,
,
此时客车走的路程为350km,出租车的路程为450km
![]() 丙城与M城之间的距离为90km
丙城与M城之间的距离为90km
方案一:小王需要的时间是![]()
方案二:小王需要的时间是![]()
![]() 小王选择方案二能更快到达乙城.
小王选择方案二能更快到达乙城.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
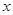 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
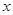 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )

A.π
B.
 π
π
C. π
π
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,数轴上的点A、B分别表示数a、b,则点A、B(点B在点A的右侧)之间的距离表示为AB=b﹣a,若点C对应的数为c,满足|a+3|+(c﹣9)2=0.
(1)写出AC的值 .
(2)如图②,点D在点C的右侧且距离m(m>0)个单位,点B在线段AC上,满足AB+AC=BD,求AB的值(用含有m的代数式表示).
(3)如图③,若点D在点C的右侧6个单位处,点P从点A出发以2个单位/秒的速度向右运动,同时点M从点C出发以1个单位/秒的速度也向右运动,当到达D点后以原来的速度向相反的方向运动.求经过多长时间,点P和点M之间的距离是2个单位?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似。如图,如果扇形AOB与扇形
 是相似扇形,且半径
是相似扇形,且半径  (
(  为不等于0的常数)。那么下面四个结论:①∠AOB=∠
为不等于0的常数)。那么下面四个结论:①∠AOB=∠  ;②△AOB∽△
;②△AOB∽△  ;③
;③  ;④扇形AOB与扇形
;④扇形AOB与扇形  的面积之比为
的面积之比为  。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直线y=﹣2x向上平移后,分别交y轴、x轴于A、B两点,直线AB经过点(m,n)且2m+n=6,则点O到线段AB的距离为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5㎝,AB=
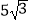 ㎝,则劣弧
㎝,则劣弧 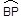 与AB,AP所围成的阴影的面积是.
与AB,AP所围成的阴影的面积是.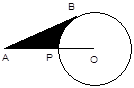
相关试题

