【题目】如图，矩形ABCD的对角线AC.BD相交于点O ， 过点O作OE⊥AC交AD于E ， 若AB=6，AD=8，求sin∠OEA的值 ．

参考答案：

【答案】解：连接EC ，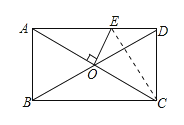

∵四边形ABCD为矩形，
∴OA=OC ， ∠ABC=90°，
利用勾股定理得：AC= =10，即OA=5，
∵OE⊥AC ，
∴AE=CE ，
在Rt△EDC中，设EC=AE=x ， 则有ED=AD-AE=8-x ， DC=AB=6，
根据勾股定理得：x2=（8-x）2+62，
解得：x= ，
∴AE= ，
在Rt△AOE中，sin∠OEA= ．
【解析】连接EC ， 由四边形ABCD为矩形，得到对角线互相平分，即O为AC中点，再由OE垂直AC ， 得到OE垂直平分AC ， 即AE=CE ， 在直角三角形EDC中，设EC=AE=x ， 利用勾股定理列出关于x的方程，求出方程的解得到EC的长，即为AE的长，利用勾股定理求出AC的长，进而求出OA的长，在直角三角形AOE中，利用锐角三角函数定义即可求出sin∠OEA的值 ．
【考点精析】通过灵活运用解直角三角形，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)即可以解答此题．

关闭