【题目】若点P(x,y)的坐标满足方程组![]()
(1)求点P的坐标(用含m,n的式子表示);
(2)若点P在第四象限,且符合要求的整数m只有两个,求n的取值范围;
(3)若点P到x轴的距离为5,到y轴的距离为4,求m,n的值(直接写出结果即可).
参考答案:
【答案】(1)P(2m﹣6,m﹣n);(2)5<n≤6;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把m、n当作已知条件,求出x、y的值即可;
(2)先求出每个不等式的解集,再求出不等式组的解集,最后根据已知得出关于n的不等式组,求出即可.
(3)根据点到x轴的距离等于该点纵坐标的绝对值,点到y轴的距离等于该点横坐标的绝对值作答.
解:(1)∵解方程组![]() 得:
得:![]() ,
,
∴P(2m﹣6,m﹣n);
(2)∵点P在第四象限,且符合要求的整数只有两个,
由![]() ,得3<m<n
,得3<m<n
∴5<n≤6
(3)∵点P到x轴的距离为5,到y轴的距离为4
∴|m﹣n|=5,|2m﹣6|=4
解得:![]() 或
或![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度
(1)当t=2时,CD=______,AD=______;(请直接写出答案)
(2)当△CBD是直角三角形时,t=______;(请直接写出答案)
(3)求当t为何值时,△CBD是等腰三角形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣4,5),C(﹣3,0).将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A'B'C',其中点A',B',分别为点A,B,C的对应点.
(1)请在所给坐标系中画出△A'B'C',并直接写出点C'的坐标;
(2)若AB边上一点P经过上述平移后的对应点为P'(x,y),用含x,y的式子表示点P的坐标;(直接写出结果即可)
(3)求△A'B'C'的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)写出(1)中利润最大的方案,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,已知
 ,其中
,其中 满足
满足 .
.(1)填空:
 = _____ ,
= _____ , = _____ ;
= _____ ;(2)如果在第三象限内一点
 ,请用含
,请用含 的式子表示⊿
的式子表示⊿ 的面积;
的面积;(3)若⑵条件下,当
 时,在坐标轴上一点
时,在坐标轴上一点 ,使得⊿
,使得⊿ 的面积与⊿
的面积与⊿ 的面积相等,请求出点
的面积相等,请求出点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 的垂直平分线
的垂直平分线 交
交 于点
于点 ,交
,交 于点
于点 .
.(1)若
 ,求
,求 的度数;
的度数;(2)若
 ,
,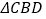 的周长为
的周长为 ,求
,求 的长.
的长.
相关试题

