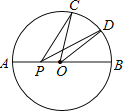
【题目】如图,已知⊙O的半径为2,C、D是直径AB同侧圆周上的两点,弧AC的度数是100°,D为弧BC的中点,动点P在直径AB上,则PC+PD的最小值是 .
参考答案:
【答案】2![]()
【解析】
试题分析:作点D关于AB的对称点D′,连接CD′与AB的交点即为所求的点P,CD′的长度为PC+PD的最小长度,求出弧BC的度数,再求出弧BD的度数,从而得到弧CD′的度数,连接OD′,过点O作OE⊥CD′,然后根据垂径定理求解即可.
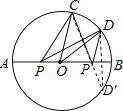
解:如图,作点D关于AB的对称点D′,连接CD′,
由轴对称确定最短路线问题,CD′与AB的交点即为所求的点P,CD′的长度为PC+PD的最小长度,
∵弧AC的度数为100°,
∴弧BC的度数为180°﹣100°=80°,
∵弧BC=2弧BD,
∴弧BD的度数=![]() ×80°=40°,
×80°=40°,
∴弧CD′的度数=80°+40°=120°,
连接OD′,过点O作OE⊥CD′,
则∠COD′=120°,OE垂直平分CD′,
∴CD′=2CE=2×![]() ×2=2
×2=2![]() .
.
∴PC+PD的最小值是2![]() .
.
故答案为:2![]() .
.
-
科目: 来源: 题型:
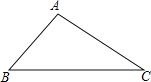
查看答案和解析>>【题目】如图,已知△ABC.
(1)利用直尺和圆规,按照下列要求作图(保留作图痕迹,不要求写作法)
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线分别交AB、BC于点E、F.
(2)连接DE,请判断线段DE与线段BF的数量关系,并说明理由.
-
科目: 来源: 题型:
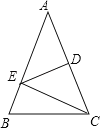
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.

(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
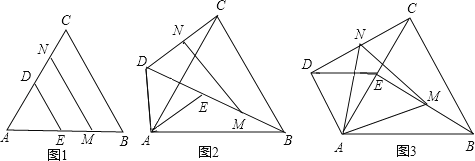
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列式中的x的值.(2x+1)2= 9.
相关试题

