【题目】如图,已知△ABC.
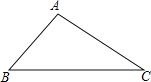
(1)利用直尺和圆规,按照下列要求作图(保留作图痕迹,不要求写作法)
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线分别交AB、BC于点E、F.
(2)连接DE,请判断线段DE与线段BF的数量关系,并说明理由.
参考答案:
【答案】(1)见解析;(2)DE=BF.
【解析】
试题分析:(1)直接利用角平分线的作法以及结合线段垂直平分线的画法得出答案;
(2)利用线段垂直平分线的性质结合全等三角形的判定与性质得出答案.
解:(1)如图所示:
(2)DE=BF,
理由:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵EF垂直平分BD,设垂足为O,
则OB=OD,BE=DE,
∴∠ABD=∠EDB,
∴∠DBC=∠EDB,
在△BOF和△DOE中,
 ,
,
∴△BOF≌△DOE(ASA),
∴DE=BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料并回答问题:
在解分式方程
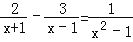 时,小明的解法如下:
时,小明的解法如下:解:方程两边同乘以(x+1)(x﹣1),得2(x﹣1)﹣3=1①
去括号,得2x﹣1=3﹣1 ②
解得x=

检验:当x=
 时,(x+1)(x﹣1)≠0 ③
时,(x+1)(x﹣1)≠0 ③所以x=
 是原分式方程的解 ④
是原分式方程的解 ④(1)你认为小明在哪里出现了错误 (只填序号)
(2)针对小明解分式方程出现的错误和解分式方程中的其他重要步骤,请你提出三条解分式方程时的注意事项;
(3)写出上述分式方程的正确解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN= 时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.
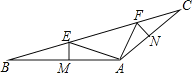
(1)求∠BAC的度数;
(2)求S△EAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
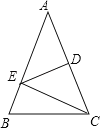
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?

-
科目: 来源: 题型:
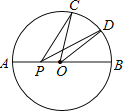
查看答案和解析>>【题目】如图,已知⊙O的半径为2,C、D是直径AB同侧圆周上的两点,弧AC的度数是100°,D为弧BC的中点,动点P在直径AB上,则PC+PD的最小值是 .
相关试题

