【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
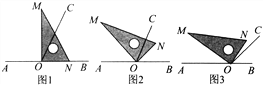
(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
参考答案:
【答案】(1)25°(2)25°(3)70°
【解析】试题分析:(1)根据∠MON和∠BOC的度数可以得到∠MON的度数;
(2)根据角平分线的性质,由∠BOC=65°,可以求得∠BOM的度数,然后由∠NOM-90°,可得∠BON的度数,从而得解;
(3)由∠BOC=65°,∠NOM=90°,∠NOC=![]() ∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.
∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.
试题解析:(1)![]() ∠MON=90,∠BOC=65°
∠MON=90,∠BOC=65°
![]() ∠MOC=∠MON-∠BOC=90°-65°=25°
∠MOC=∠MON-∠BOC=90°-65°=25°
(2)![]() ∠BOC=65°,OC平分∠MOB
∠BOC=65°,OC平分∠MOB
![]() ∠MOB=2∠BOC=130°
∠MOB=2∠BOC=130°
![]() ∠BON=∠MOB-∠MON=130°-90°=40°
∠BON=∠MOB-∠MON=130°-90°=40°
![]() ∠CON=∠COB-∠BON=65°-40°=25°
∠CON=∠COB-∠BON=65°-40°=25°
(3)![]() ∠NOC=
∠NOC=![]() ∠AOM
∠AOM ![]() ∠AOM=4∠NOC
∠AOM=4∠NOC ![]() ∠BOC=65°
∠BOC=65°
![]() ∠AOC=∠AOB-∠BOC=180°-65°=115°
∠AOC=∠AOB-∠BOC=180°-65°=115°
![]() ∠MON=90°
∠MON=90°
![]() ∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°
∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°
![]() 4∠NOC+∠NOC=25°
4∠NOC+∠NOC=25°
![]() ∠NOC=5°
∠NOC=5°
![]() ∠NOB=∠NOC+∠BOC=70°
∠NOB=∠NOC+∠BOC=70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.
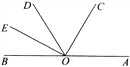
(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.
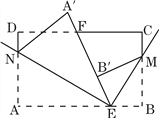
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知10m=3,10n=2,求103m_2n的值;
(2)已知2x+5y-3=0,求4x·32y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1100元,那么此人住院的医疗费是( )
住院医疗费(元)
报销率(%)
不超过500元的部分
0
超过500~1000元的部分
60
超过1000~3000元的部分
80
……
A.1000元
B.1250元
C.1500元
D.2000元 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的有( )
①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等④若a2=b2,则a=b;⑤若a>b,则ac2>bc2.
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
相关试题

