【题目】已知关于x的一元二次方程x2﹣6x+2m+1=0有实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2+x1+x2=15,求m的值.
参考答案:
【答案】(1)m≥4 (2)m=4
【解析】试题分析:(1)由根的判别式△≥0来求实数m的取值范围;(2)直接利用根与系数的关系解答.
试题解析:(1)由题意得,△=(﹣6)2﹣4(2m+1)≥0,解得m≥4;(2)∵关于x的一元二次方程x2﹣6x+2m+1=0的两个实数根为x1,x2,∴x1x2=2m+1,x1+x2=6,∴x1x2+x1+x2=2m+1+6=15,解得m=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+2x﹣1
(1)用配方法或公式法求出它的顶点坐标和对称轴.
(2)直接写出它与y轴的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空:单项式2.7×103a2b的系数是________,次数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
其中正确的有__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算6a6÷3a2的结果为( )
A. 3a4B. 3a3C. 2a3D. 2a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、C、B三点在同一条直线上,△DAC和△EBC都等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:① △ACE≌△DCB;② CM=CN;③ AC=DN. 其中,正确结论的个数是( ).
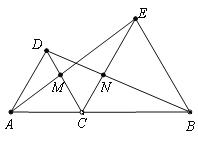
A. 3个 B. 2个 C. 1个 D. 0个
相关试题

