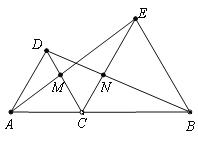
【题目】如图，A、C、B三点在同一条直线上，△DAC和△EBC都等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：① △ACE≌△DCB；② CM＝CN；③ AC＝DN. 其中，正确结论的个数是（ ）.

A. 3个 B. 2个 C. 1个 D. 0个

参考答案：

【答案】B

【解析】试题分析：根据等边三角形的性质和全等三角形的判定与性质采用排除法对各个结论进行分析从而得出答案．

∵△DAC和△EBC都是等边三角形

∴AC=CD，CE=BC，∠ACD=∠ECB=60°

∴∠ACE=∠DCB

∴△ACE≌△DCB（SAS）（①正确）

∴∠AEC=∠DBC

∵∠DCE+∠ACD+∠ECB=180°，∠ACD=∠ECB=60°

∴∠DCE=∠ECB=60°

∵CE=BC，∠DCE=∠ECB=60°，∠AEC=∠DBC

∴△EMC≌△BNC（ASA）

∴CM=CN（②正确）

∵AC="DC" 在△DNC中，DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC＞60°，而DN所对的角为60°，根据三角形中等边对等角、大边对大角，小边对小角的规律，则DC＞DN，即是AC＞DN，所以③错误，所以正确的结论有两个．

故选B．

关闭