【题目】一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.

参考答案:
【答案】当∠C为钝角时,![]() ; 当∠B为钝角时,
; 当∠B为钝角时,![]()
【解析】
试题(3)如图过A作AD⊥BC于D,则BD=BC+CD=a+CD

在△ABD中:AD2=AB2-BD2
在△ACD中:AD2=AC2-CD2
AB2-BD2= AC2-CD2
c2-(![]() +CD)2= b2-CD2
+CD)2= b2-CD2
∴![]()
∵![]() >0,CD>0
>0,CD>0
∴![]() ,所以:
,所以:![]()
在△ABC中,BC=a=3,CA=b=4,AB=c;若△ABC是钝角三角形 , 当∠C为钝角时,![]() ,c<a+b=7,所以
,c<a+b=7,所以![]() ;
;
当∠B为钝角时,![]() ,解得
,解得![]() ,又因为c>b-a=1,所以
,又因为c>b-a=1,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以
 ,
,  ,
,  的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以
 ,
,  ,
,  的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形其中所有正确结论的序号为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一架方梯AB长25米,如图所示,斜靠在一面上:
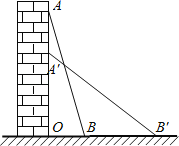
(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D.

(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),连接BC.

(1)求该抛物线的解析式和对称轴,并写出线段BC的中点坐标;
(2)将线段BC先向左平移2个单位长度,再向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,求此时点C1的坐标和m的值;
(3)若点P是该抛物线上的动点,点Q是该抛物线对称轴上的动点,当以P,Q,B,C四点为顶点的四边形是平行四边形时,求此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )

A.
B.
C.
D.
相关试题

