搜索
【题目】如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ） 
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：如图所示：设BC=x， ∵在Rt△ABC中，∠B=90°，∠A=30°，
∴AC=2BC=2x，AB= 
BC= x，
根据题意得：AD=BC=x，AE=DE=AB= x，
作EM⊥AD于M，则AM= 
AD= x，
在Rt△AEM中，cos∠EAD= 
= 
= 
；
故选：B．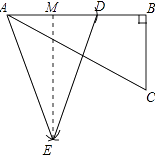
设BC=x，由含30°角的直角三角形的性质得出AC=2BC=2x，求出AB= BC= x，根据题意得出AD=BC=x，AE=DE=AB= x，作EM⊥AD于M，由等腰三角形的性质得出AM= AD= x，在Rt△AEM中，由三角函数的定义即可得出结果．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一、阅读理解：
在△ABC中，BC=a，CA=b，AB=c；
（1）若∠C为直角，则a2+b2=c2；
（2）若∠C为锐角，则a2+b2与c2的关系为：a2+b2＞c2；
（3）若∠C为钝角，试推导a2+b2与c2的关系．
二、探究问题：在△ABC中，BC=a=3，CA=b=4，AB=c，若△ABC是钝角三角形，求第三边c的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是大半圆O的直径，AO是小半圆M的直径，点P是大半圆O上一点，PA与小半圆M交于点C，过点C作CD⊥OP于点D．
（1）求证：CD是小半圆M的切线；
（2）若AB=8，点P在大半圆O上运动（点P不与A，B两点重合），设PD=x，CD2=y． ①求y与x之间的函数关系式，并写出自变量x的取值范围；
②当y=3时，求P，M两点之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx﹣3a（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），连接BC．
（1）求该抛物线的解析式和对称轴，并写出线段BC的中点坐标；
（2）将线段BC先向左平移2个单位长度，再向下平移m个单位长度，使点C的对应点C1恰好落在该抛物线上，求此时点C1的坐标和m的值；
（3）若点P是该抛物线上的动点，点Q是该抛物线对称轴上的动点，当以P，Q，B，C四点为顶点的四边形是平行四边形时，求此时点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的图象如图所示，则|a﹣b+c|+|2a+b|=（ ）
A.a+b
B.a﹣2b
C.a﹣b
D.3a -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BCAD=
AE2；④S△ABC=4S△ADF ． 其中正确的有（ ） 
A.1个
B.2 个
C.3 个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（ ）
A.
B.
C.
D.
相关试题
